
分析 由$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,可得△ABC的重心是F,从而y1+y2+y3=0,利用斜率公式,即可求得结论.
解答 解:设A、B、C三点的坐标分别为(x1,y1),(x2,y2),(x3,y3),
且x1=$\frac{{{y}_{1}}^{2}}{2p}$,x2=$\frac{{{y}_{2}}^{2}}{2p}$,x3=$\frac{{{y}_{3}}^{2}}{2p}$.
则∵$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,
∴△ABC的重心是F,
∵抛物线y2=2px的焦点F的坐标为F($\frac{p}{2}$,0),
∴y1+y2+y3=0,
∴$\frac{1}{{{k_{{A}{B}}}}}+\frac{1}{{{k_{{B}C}}}}+\frac{1}{{{k_{C{A}}}}}$=$\frac{{y}_{2}+{y}_{1}}{2p}$+$\frac{{y}_{2}+{y}_{3}}{2p}$+$\frac{{y}_{1}+{y}_{3}}{2p}$=$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{p}$=0.
故答案为:0
点评 本题主要考查抛物线的性质,同时考查向量知识的运用,运用斜率公式和三角形的重心是解题的关键,属于中档题.


科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(文)试卷(解析版) 题型:选择题
已知集合 ,若对于任意
,若对于任意 ,存在
,存在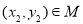 ,使得
,使得 成立,则称集合
成立,则称集合 是“理想集合”.给出下列4个集合:
是“理想集合”.给出下列4个集合:
① ;
;
② ;
;
③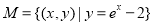 ;
;
④ .
.
其中所有“理想集合”的序号是( )
A.①③ B.②③
C.②④ D.③④
查看答案和解析>>
科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(理)试卷(解析版) 题型:选择题
设双曲线
 的右焦点为
的右焦点为 ,过点
,过点 与
与 轴垂直的直线
轴垂直的直线 交两渐近线于
交两渐近线于 ,
, 两点,与双曲线的其中一个交点为
两点,与双曲线的其中一个交点为 ,设坐标原点为
,设坐标原点为 ,若
,若
 ,且
,且 ,则该双曲线的渐近线为( )
,则该双曲线的渐近线为( )
A. B.
B. C.
C. D.
D. 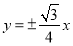
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 48 | C. | 56 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com