
| A. | 33 | B. | 34 | C. | 35 | D. | 36 |
分析 先利用条件求出数列{cn}的通项公式,证明其满足“亚三角形”数列.然后利用对数型复合函数的单调性得到g(cn)是单调递减函数,再由lgcn+4+lgcn+2>lgcn求解对数不等式得答案.
解答 解:由5Sn+1-4Sn=10080,得
5Sn-4Sn-1=10080(n≥2),两式作差得:5cn+1-4cn=0(n≥2).
∴$\frac{{c}_{n+1}}{{c}_{n}}=\frac{4}{5}$(n≥2).
又c1=2016,且5Sn+1-4Sn=10080,
∴5(c1+c2)-4c1=10080,解得,${c}_{2}=\frac{8064}{5}$.
∴$\frac{{c}_{2}}{{c}_{1}}=\frac{\frac{8064}{5}}{2016}=\frac{4}{5}$.
则数列{cn}是等比数列.
∴${c}_{n}=2016•(\frac{4}{5})^{n-1}$.
由上可知,数列{cn}是递减数列.
∵${c}_{n+4}+{c}_{n+2}=2016•(\frac{4}{5})^{n+3}+2016•(\frac{4}{5})^{n+1}$=$\frac{656}{625}•2016•(\frac{4}{5})^{n-1}>2016•(\frac{4}{5})^{n-1}={c}_{n}$.
∴数列{cn}是“亚三角形”数列;
函数g(x)=lgx是增函数,则lgcn是减函数.
由lgcn+4+lgcn+2>lgcn得,$lg2016+(n+3)lg\frac{4}{5}+lg2016+(n+1)lg\frac{4}{5}$$>lg2016+(n-1)lg\frac{4}{5}$.
整理得:$(n+5)lg\frac{4}{5}>-lg2016$.
解得:n<33.04.
则数列{cn}的项数的最大值为33.
故选:A.
点评 本题是在新定义下对数列的综合考查,考查了对数函数的单调性.关于新定义的题型,在作题过程中一定要理解定义,并会用定义来解题,是中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
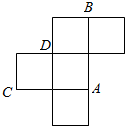 如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.
如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{2}{3}$x | B. | y=±$\frac{4}{9}$x | C. | y=±$\frac{3}{2}$x | D. | y=±$\frac{9}{4}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com