Question

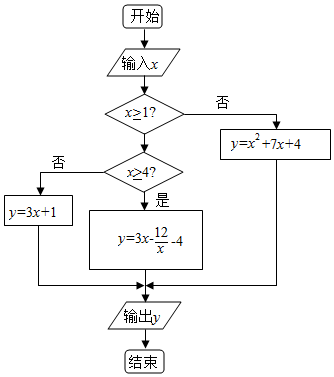
15．一个算法流程图如图所示，要使输出的y值是输入的x值的2倍，这样的x值的个数是（　　）

• A． 1
• B． 3
• C． 5
• D． 6

Answer 1

分析 模拟执行程序，可得程序的功能是计算并输出y=$\left\{\begin{array}{l}{\stackrel{{x}^{2}+7x+4}{3x+1}}&{\stackrel{x＜1}{1≤x＜4}}\\{3x-\frac{12}{x}-4}&{x≥4}\end{array}\right.$的值，根据条件，分x＜1，1≤x＜4，x≥4三种情况分别讨论，满足输出的y值是输入的x值的2倍的情况，即可得到答案．

解答 解：模拟执行程序，可得程序的功能是计算并输出y=$\left\{\begin{array}{l}{\stackrel{{x}^{2}+7x+4}{3x+1}}&{\stackrel{x＜1}{1≤x＜4}}\\{3x-\frac{12}{x}-4}&{x≥4}\end{array}\right.$的值．
当x＜1时，由x²+7x+4=2x，解得：x=-4，-1满足条件；
当1≤x＜4时，由3x+1=2x，可得：x无解；
当x≥4时，由3x$-\frac{12}{x}$-4=2x，解得：x=6，或-2（舍去），
故这样的x值有3个．
故选：B．

点评 本题主要考查根据流程图（或伪代码）写程序的运行结果，我们要先分析流程图（或伪代码）判断其功能，并将其转化为数学问题，建立数学模型后，用数学的方法解答即可得到答案，属于基础题．