
分析 由条件里用正弦定理、两角和的正弦公式求得cosC,进而可求C,根据△ABC的面积公式和已知,求得c=3ab.再由余弦定理化简可得9a2b2=a2+b2+ab≥3ab,由此求得c的最小值.
解答 解:在△ABC中,由条件里用正弦定理可得sinCcosB=sinA+$\frac{1}{2}$sinB=sin(B+C)+$\frac{1}{2}$sinB,
即 2sinCcosB=2sinBcosC+2sinCcosB+sinB,
∴2sinBcosC+sinB=0,
∴cosC=-$\frac{1}{2}$,C=$\frac{2π}{3}$.
由于△ABC的面积为S=$\frac{1}{2}$ab•sinC=$\frac{\sqrt{3}}{4}$ab=$\frac{\sqrt{3}}{12}$c,
∴c=3ab.
再由余弦定理可得c2=a2+b2-2ab•cosC,整理可得:9a2b2=a2+b2+ab≥3ab,
当且仅当a=b时,取等号,
∴ab≥$\frac{1}{3}$,可得:c=3ab≥1,即边c的最小值为1.
故答案为:1.
点评 本题主要考查正弦定理和余弦定理的应用,诱导公式、两角和的正弦公式、基本不等式的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
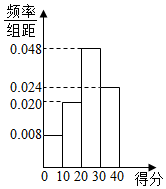 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如表所示:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如表所示:| 分值 | [0,10) | [10,20) | [20,30) | [30,40) |
| 场数 | 10 | 20 | 40 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
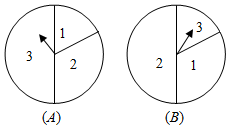 如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.
如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x,y∈R,x,y全不为0,则x2+y2≠0 | B. | 若x,y∈R,x,y不全为0,则x2+y2=0 | ||
| C. | 若x,y∈R,x,y不全为0,则x2+y2≠0 | D. | 若x,y∈R,x,y全为0,则x2+y2≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com