
| 优秀 | 不优秀 | 总计 | |
| 甲队 | 80 | 240 | 320 |
| 乙队 | 40 | 200 | 240 |
| 合计 | 120 | 440 | 560 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)计算K2,与临界值比较,即可判断能否在犯错误的概率不超过0.025的前提下认为运动员的测试成绩与所双在训练队有关系;
(Ⅱ)求出基本事件的个数,利用古典概型概率公式,可得结论.
解答 解:(Ⅰ)由题意得$k=\frac{{560×{{(80×200-40×240)}^2}}}{120×440×320×240}≈5.657$>5.024,…(2分)
所以能在犯错误的概率不超过0.025的前提下认为运动员的测试成绩与所在训练队有关系.…(3分)
(Ⅱ)集训队6名队员中有甲队4人,乙队2人 …(4分)
从这6名运动员中任取2名运动员参加比赛,有C62=15种情况…(8分)
记事件A为“选取的2名队员来自不同训练队”,事件A所包含的搭配情况,共有C41C21=8种情况…(10分)
所以P(A)=$\frac{8}{15}$ …(12分)
点评 本题主要考查概率的计算、独立性检验的应用,解题的关键是正确运算出观测值,理解临界值对应的概率的意义,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ${A}_{n}^{51}$ | B. | ${C}_{n}^{51}$ | C. | ${A}_{n}^{50}$ | D. | ${C}_{n}^{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
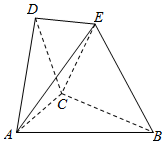 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com