
分析 (Ⅰ)求出g(x)的导数,得到g(1),g′(1),根据系数相等求出a,b的值即可;
(Ⅱ)求出x1,x2是方程x2-ax+a=0的根,得到x1+x2=a,x1•x2=a,根据△>0,求出a>4,于是g(x1)+g(x2)+4=alna-$\frac{1}{2}$a2-a+4,令h(x)=xlnx-$\frac{1}{2}$x2-x+4,(x>4),根据函数的单调性求出h(x)<h(4),从而证出结论.
解答 解:(Ⅰ)函数g(x)=alnx+$\frac{1}{2}$x2+(1-b)x,x>0,
g′(x)=$\frac{a}{x}$+x+(1-b),g(1)=$\frac{3}{2}$-b,g′(1)=a-b+2,
∴切线方程是:y-$\frac{3}{2}$+b=(a-b+2)(x-1),
即:2(a-b+2)x-2y-2a-1=0,
又切线方程为8x-2y-3=0,
∴$\left\{\begin{array}{l}{a-b+2=4}\\{2a+1=3}\end{array}\right.$,解得:a=1,b=-1;
(Ⅱ)若b=a+1,则g(x)=alnx+$\frac{1}{2}$x2-ax,(x>0),
g′(x)=$\frac{a}{x}$+x-a=$\frac{{x}^{2}-ax+a}{x}$,(x>0),
若x1,x2是函数g(x)的两个极值点,
则x1,x2是方程x2-ax+a=0的根,
∴x1+x2=a,x1•x2=a,
而△=a2-4a>0,解得:a>4或a<0,
显然a>4,
∴g(x1)+g(x2)+4=alnx1+$\frac{1}{2}$${{x}_{1}}^{2}$-ax1+alnx2+$\frac{1}{2}$${{x}_{2}}^{2}$-ax2+4=alna-$\frac{1}{2}$a2-a+4,
令h(x)=xlnx-$\frac{1}{2}$x2-x+4,(x>4),
h′(x)=lnx-x,h″(x)=$\frac{1-x}{x}$<0,
∴h′(x)在(4,+∞)递减,
∴h′(x)max>h′(4)=ln4-4<0,
∴h(x)在(4,∞)递减,
∴h(x)<h(4)=8(ln2-1)<0,
∴g(x1)+g(x2)+4<0.
点评 本题考查了曲线的切线方程问题,考查二次函数的性质,导数的应用以及函数恒成立问题,是一道中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
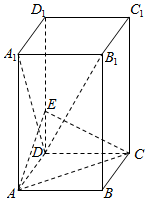 如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.
如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 不优秀 | 总计 | |
| 甲队 | 80 | 240 | 320 |
| 乙队 | 40 | 200 | 240 |
| 合计 | 120 | 440 | 560 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
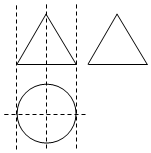 如图,某几何体的正视图和侧视图都是正三角形,俯视图是圆,若该几何体的表面积S=π,则它的体积V=( )
如图,某几何体的正视图和侧视图都是正三角形,俯视图是圆,若该几何体的表面积S=π,则它的体积V=( )| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{π}{9}$ | D. | $\frac{π}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com