
分析 (1)利用an=Sn-Sn-1及(Sn-1)2=anSn整理可知Sn=$\frac{1}{2-{S}_{n-1}}$,通过计算出前三项的值,利用归纳推理猜想Sn=$\frac{n}{n+1}$,进而利用数学归纳法证明即可;
(2)通过(1)裂项可知bn=(-1)n+1($\frac{1}{n}$-$\frac{1}{n+2}$),进而分n为奇数、偶数两种情况讨论即可;
(3)通过(1)可知cn=$\frac{1}{n}$,进而问题转化为求首项为1、公比为$\frac{1}{2}$的等比数列的前n项和.
解答 解:(1)∵an=Sn-Sn-1,
∴(Sn-1)2=anSn=(Sn-Sn-1)Sn,即Sn=$\frac{1}{2-{S}_{n-1}}$,
又∵(S1-1)2=S12,即S1=$\frac{1}{2}$,
∴S2=$\frac{1}{2-\frac{1}{2}}$=$\frac{2}{3}$,S3=$\frac{1}{2-\frac{2}{3}}$=$\frac{3}{4}$,
…
猜想:Sn=$\frac{n}{n+1}$.
下面用数学归纳法来证明:
①当n=1时,命题成立;
②假设当n=k(k≥1)时,有Sk=$\frac{k}{k+1}$,
则Sk+1=$\frac{1}{2-\frac{k}{k+1}}$=$\frac{k+1}{k+2}$,
即当n=k+1时,命题也成立;
由①②可知Sn=$\frac{n}{n+1}$.
∴an=Sn-Sn-1=$\frac{n}{n+1}$-$\frac{n-1}{n}$=$\frac{1}{n(n+1)}$(n≥2),
又∵a1=S1=$\frac{1}{2}$满足上式,
∴数列{an}的通项公式an=$\frac{1}{n(n+1)}$;
(2)由(1)可知,bn=(-1)n+1•(an+an+1)=(-1)n+1($\frac{1}{n}$-$\frac{1}{n+2}$),
特别地,当n为奇数时,n+1为偶数,此时bn+bn+1=$\frac{1}{n}$-$\frac{1}{n+2}$-$\frac{1}{n+1}$+$\frac{1}{n+3}$,
①若n为偶数,则Tn=(b1+b2)+(b3+b4)+…+(bn-1+bn)
=(1-$\frac{1}{3}$-$\frac{1}{2}$+$\frac{1}{4}$)+($\frac{1}{3}$-$\frac{1}{5}$-$\frac{1}{4}$+$\frac{1}{6}$)+…+($\frac{1}{n-1}$-$\frac{1}{n+1}$-$\frac{1}{n}$+$\frac{1}{n+2}$)
=1-$\frac{1}{2}$-$\frac{1}{n+1}$+$\frac{1}{n+2}$
=$\frac{1}{2}$-$\frac{1}{(n+1)(n+2)}$;
②当n为奇数且n>1时,Tn=Tn-1+bn,
故Tn=$\frac{1}{2}$-$\frac{1}{n(n+1)}$+$\frac{1}{n}$-$\frac{1}{n+2}$=$\frac{1}{2}$+$\frac{1}{(n+1)(n+2)}$,
又∵T1=b1=$\frac{2}{3}$满足上式,
∴当n为奇数时,Tn=$\frac{1}{2}$+$\frac{1}{(n+1)(n+2)}$;
由①②可知:Tn=$\left\{\begin{array}{l}{\frac{1}{2}+\frac{1}{(n+1)(n+2)},}&{n为奇数}\\{\frac{1}{2}-\frac{1}{(n+1)(n+2)},}&{n为偶数}\end{array}\right.$;
(3)由(1)可知an=$\frac{1}{n(n+1)}$,
∴cn=(n+1)•an=$\frac{1}{n}$(n∈N*),
由题意可知需等比数列{dn}的首项及公比均达到最大,显然首项为1、公比为$\frac{1}{2}$,
∴1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$=2(1-$\frac{1}{{2}^{n}}$),
∵$\underset{lim}{n→∞}$(1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$)=$\underset{lim}{n→∞}$[2(1-$\frac{1}{{2}^{n}}$)]=2,
∴M的最小值为2.
点评 本题考查数列的通项及前n项和,考查分类讨论的思想,考查数学归纳法,注意解题方法的积累,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
 已知平行四边形ABCD中,∠A=45°,且AB=BD=1,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示:
已知平行四边形ABCD中,∠A=45°,且AB=BD=1,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}π}}{3}$ | B. | $\frac{{\sqrt{6}π}}{3}$ | C. | $\frac{{2\sqrt{3}π}}{3}$ | D. | $\frac{{2\sqrt{6}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
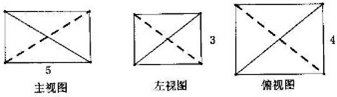 一个三棱锥的三视图如图所示,则该棱锥的外接球的体积为( )
一个三棱锥的三视图如图所示,则该棱锥的外接球的体积为( )| A. | 1000$\sqrt{2}$π | B. | 125$\sqrt{2}$π | C. | $\frac{1000\sqrt{2}π}{3}$ | D. | $\frac{125\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{{(10+2\sqrt{2})π}}{2}+1$ | B. | $\frac{13π}{6}$ | C. | $\frac{{(11+\sqrt{2})π}}{2}+1$ | D. | $\frac{{(11+2\sqrt{2})π}}{2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com