
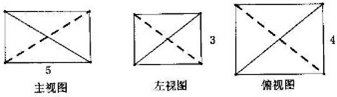
 一个三棱锥的三视图如图所示,则该棱锥的外接球的体积为( )
一个三棱锥的三视图如图所示,则该棱锥的外接球的体积为( )| A. | 1000$\sqrt{2}$π | B. | 125$\sqrt{2}$π | C. | $\frac{1000\sqrt{2}π}{3}$ | D. | $\frac{125\sqrt{2}π}{3}$ |
分析 由三视图可知该三棱锥:为棱长为5、4、3的长方体切去四个小棱锥得到的几何体,得该三棱锥和长方体的外接球相同,利用长方体的体对角线是球的直径求出R,代入球的体积公式计算即可.
解答 解: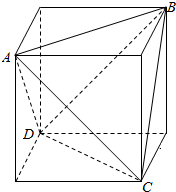 由三视图可知该三棱锥:
由三视图可知该三棱锥:
为棱长为5、4、3的长方体切去四个小棱锥得到的几何体,
∴该三棱锥和长方体的外接球相同,
设该三棱锥的外接球半径为R,
∴2R=$\sqrt{{5}^{2}+{4}^{2}+{3}^{2}}$=5$\sqrt{2}$.∴R=$\frac{5\sqrt{2}}{2}$,
∴外接球的体积为V=$\frac{4}{3}π{R}^{3}$=$\frac{125\sqrt{2}π}{3}$,
故选:D.
点评 本题考查了几何体的三视图,常见几何体与外接球的关系,根据三视图得出三棱锥与长方体的关系是关键,考查空间想象能力.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
 如图所示,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AB∥CD,AB⊥AD,AB=2AD=2AP=2CD=2,E是棱PC上一点,且CE=2PE.
如图所示,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AB∥CD,AB⊥AD,AB=2AD=2AP=2CD=2,E是棱PC上一点,且CE=2PE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 工作 效益 机器 | 一 | 二 | 三 | 四 | 五 |
| 甲 | 15 | 17 | 14 | 17 | 15 |
| 乙 | 22 | 23 | 21 | 20 | 20 |
| 丙 | 9 | 13 | 14 | 12 | 10 |
| 丁 | 7 | 9 | 11 | 9 | 11 |
| 戊 | 13 | 15 | 14 | 15 | 11 |
| A. | 甲只能承担第四项工作 | B. | 乙不能承担第二项工作 | ||
| C. | 丙可以不承担第三项工作 | D. | 获得的效益值总和为78 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
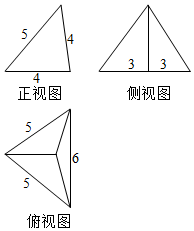
| A. | $\frac{{15\sqrt{39}}}{2}$ | B. | $\frac{{5\sqrt{39}}}{2}$ | C. | $5\sqrt{39}$ | D. | $5\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com