
已知抛物线 与双曲线
与双曲线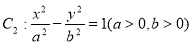 有公共焦点
有公共焦点 .点
.点 是曲线C1,C2在第一象限的交点,且
是曲线C1,C2在第一象限的交点,且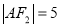 .
.
(1)求双曲线交点 及另一交点
及另一交点 的坐标和点
的坐标和点 的坐标;
的坐标;
(2)求双曲线 的方程;
的方程;
(3)以 为圆心的圆M与直线
为圆心的圆M与直线 相切,圆N:
相切,圆N: ,过点P(1,
,过点P(1, )作互相垂直且分别与圆M、圆N相交的直线
)作互相垂直且分别与圆M、圆N相交的直线 和
和 ,设
,设 被圆M截得的弦长为s,
被圆M截得的弦长为s, 被圆N截得的弦长为t,问:
被圆N截得的弦长为t,问: 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
(1) 、
、 ,点A的坐标为
,点A的坐标为 或
或 ;(2)
;(2) ;(3)
;(3) 为定值.说明如下:设圆M的方程为:
为定值.说明如下:设圆M的方程为: ,因为圆M与直线
,因为圆M与直线 相切,所以圆M的半径为
相切,所以圆M的半径为 .故圆M:
.故圆M:  .显然,当直线
.显然,当直线 的斜率不存在时不符合题意,
的斜率不存在时不符合题意,
所以直线 的斜率存在,设
的斜率存在,设 的方程为
的方程为 ,即
,即 .
.
设 的方程为
的方程为 ,即
,即 .
.
所以点 到直线
到直线 的距离为
的距离为 ,点
,点 到直线
到直线 的距离为
的距离为 ,所以直线
,所以直线 被圆M截得的弦长
被圆M截得的弦长 ,直线
,直线 被圆M截得的弦长
被圆M截得的弦长 ,所以
,所以 .
.
【解析】
试题分析:(1)由抛物线 的焦点能求出双曲线交点
的焦点能求出双曲线交点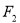 及另一交点
及另一交点 的坐标,由抛物线定义能求出点A的坐标;(2)由已知条件推导出
的坐标,由抛物线定义能求出点A的坐标;(2)由已知条件推导出 ,由此能求出双曲线
,由此能求出双曲线 的方程;(3)设圆M的方程为:
的方程;(3)设圆M的方程为: ,设直线
,设直线 的方程为
的方程为 ,设
,设 的方程为
的方程为 ,由此利用点到直线距离公式结合已知条件能求出
,由此利用点到直线距离公式结合已知条件能求出 是定值
是定值 .
.
试题解析:(1)因为 的焦点为
的焦点为 ,所以双曲线
,所以双曲线 的焦点为
的焦点为 、
、 .设
.设 ,由
,由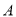 点在抛物线
点在抛物线 上,且
上,且 ,由抛物线的定义得,
,由抛物线的定义得, ,即
,即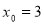 ,所以
,所以 ,即
,即 ,所以点A的坐标为
,所以点A的坐标为 或
或 .
.
(2)由题意知 ,又因为
,又因为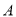 点在双曲线
点在双曲线 上,由双曲线定义得:
上,由双曲线定义得:
 ,即
,即 ,所以
,所以 ,故双曲线
,故双曲线 的方程为:
的方程为: .
.
(3) 为定值.说明如下:
为定值.说明如下:
设圆M的方程为: ,因为圆M与直线
,因为圆M与直线 相切,所以圆M的半径为
相切,所以圆M的半径为 .故圆M:
.故圆M:  .显然,当直线
.显然,当直线 的斜率不存在时不符合题意,
的斜率不存在时不符合题意,
所以直线 的斜率存在,设
的斜率存在,设 的方程为
的方程为 ,即
,即 .
.
设 的方程为
的方程为 ,即
,即 .
.
所以点 到直线
到直线 的距离为
的距离为 ,点
,点 到直线
到直线 的距离为
的距离为 ,所以直线
,所以直线 被圆M截得的弦长
被圆M截得的弦长 ,直线
,直线 被圆M截得的弦长
被圆M截得的弦长 ,所以
,所以 .
.
考点:直线与圆锥曲线的综合问题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届广东省高二下学期中段考文科数学试卷(解析版) 题型:选择题
独立性检验中,假设H0:变量X与变量Y没有关系,则在H0成立的情况下,P(K2≥6.635)≈0.010表示的意义是( )
A.在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y有关”
B.在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y无关”
C.有99%以上的把握认为“变量X与变量Y无关”
D.有99%以上的把握认为“变量X与变量Y有关”
查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末理科数学试卷(解析版) 题型:填空题
(2014•濮阳县一模)如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是 _________ .

查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末理科数学试卷(解析版) 题型:选择题
由函数y=x2的图象与直线x=1、x=2和x轴所围成的封闭图形的面积是( )
A.3 B. C.2 D.
C.2 D.
查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:填空题
在极坐标系中,圆C的方程为ρ=1,直线l的方程为ρsin(θ+ )=
)=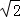 ,则圆心C到直线l的距离为 _________ .
,则圆心C到直线l的距离为 _________ .
查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:选择题
函数 在定义域R内可导,若
在定义域R内可导,若 ,且
,且 ,若
,若 ,
, ,
, ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
A.a>b>c B.c>a>b C. B>a>c D.c>b>a
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
如图所示,圆 的直径
的直径 ,
,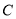 为圆周上一点,
为圆周上一点, ,过
,过 作圆
作圆 的切线
的切线 ,则点
,则点 到直线
到直线 的距离
的距离 __________.
__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com