
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() 是等边三角形,点
是等边三角形,点![]() 在
在![]() 上,且
上,且![]() .
.

(1)证明:![]() //平面
//平面![]() .
.
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,通过证明
,通过证明![]() //
//![]() ,即可推证线面平行;
,即可推证线面平行;
(2)取![]() 中点为
中点为![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,求得对应平面的法向量,利用向量法求二面角的余弦值即可.
为坐标原点建立空间直角坐标系,求得对应平面的法向量,利用向量法求二面角的余弦值即可.
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
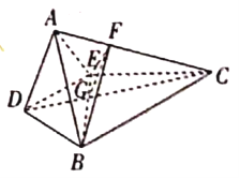
∵在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,
![]() //
//![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() //
//![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() //平面
//平面![]() .
.
(2)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,显然
,显然![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 、
、![]() 分別为
分別为![]() 、
、![]() 的中点,且在等腰梯形
的中点,且在等腰梯形![]() 中,
中,![]() ,
,
所以![]() .以
.以![]() 为原点建立如所示的空间直角坐标系
为原点建立如所示的空间直角坐标系![]() ,
,
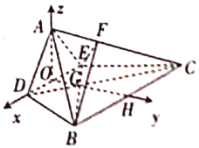
设![]() ,则
,则 ,
,
 ,
,![]() ,
, ,
,
∴ ,
,
∴![]()

易得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
可得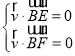 ,故
,故 ,
,
令![]() ,可得
,可得![]() ,
,![]() ,则
,则![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,则
,则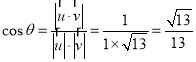 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(![]() ,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(![]() )又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足![]() .其中星等为
.其中星等为![]() 的星的亮度为
的星的亮度为![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,则与
倍,则与![]() 最接近的是(当
最接近的是(当![]() 较小时,
较小时, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与直线
与直线![]() 的直角坐标方程.
的直角坐标方程.
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 在
在![]() 轴上,
轴上,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,经过点
,经过点![]() 且垂直于
且垂直于![]() 轴的直线与抛物线
轴的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 到直线
到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某饲料厂原有陈粮10吨,又购进新粮x吨,现将粮食总库存量的一半精加工为饲料.若被精加工的新粮最多可用![]() 吨,被精加工的陈粮最多可用y2吨,记
吨,被精加工的陈粮最多可用y2吨,记![]() ,则函数
,则函数![]() 的图象为( )
的图象为( )
A.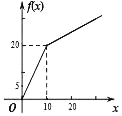 B.
B.
C.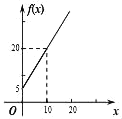 D.
D.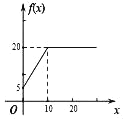
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数k和b,使得函数![]() 对其公共定义域上的任意实数x都满足:
对其公共定义域上的任意实数x都满足:![]() 恒成立,则称此直线
恒成立,则称此直线![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() (e为自然对数的底数),有下列命题:
(e为自然对数的底数),有下列命题:
①![]() 内单调递增;
内单调递增;
②![]() 之间存在“隔离直线”,且b的最小值为
之间存在“隔离直线”,且b的最小值为![]() ;
;
③![]() 之间存在“隔离直线”,且k的取值范围是
之间存在“隔离直线”,且k的取值范围是![]() ;
;
④![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]() .
.
其中真命题的序号为__________.(请填写正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术;蕴含了极致的数学美和丰富的传统文化信息,现有一幅剪纸的设计图,其中的4个小圆均过正方形的中心,且内切于正方形的两邻边.若在正方形内随机取一点,则该点取自黑色部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设一个袋子里有红、黄、蓝色小球各一个现每次从袋子里取出一个球(取出某色球的概率均相同),确定颜色后放回,直到连续两次均取出红色球时为止,记此时取出球的次数为ξ,则ξ的数学期望为_____ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com