
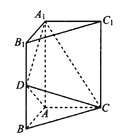
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中点.
的中点.
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 将此三棱柱分成的两部分的体积之比.
将此三棱柱分成的两部分的体积之比.
【答案】(1)平面![]() 平面
平面![]() ;(2)
;(2)![]()
【解析】试题分析:(Ⅰ)通过线面垂直可得![]() ,运用勾股定理可得
,运用勾股定理可得![]() ,由线面垂直判定定理可得
,由线面垂直判定定理可得![]() 平面
平面![]() ,由面面垂直判定定理得结论;(Ⅱ)平面
,由面面垂直判定定理得结论;(Ⅱ)平面![]() 将三棱柱分成上、下两部分,其上面部分几何体为四棱锥
将三棱柱分成上、下两部分,其上面部分几何体为四棱锥![]() ,下面部分几何体为四棱锥
,下面部分几何体为四棱锥![]() ,分别计算出其体积即可.
,分别计算出其体积即可.
试题解析:(Ⅰ)在三棱柱中,有![]() ,
,
又因为![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
,
由![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中点.
的中点.
所以![]() ,
, ![]() ,
,
则![]()
![]() ,
,
所以![]() ,
,
因![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
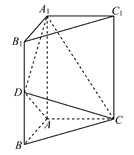
(Ⅱ)平面![]() 将三棱柱分成上、下两部分,其上面部分几何体为四棱锥
将三棱柱分成上、下两部分,其上面部分几何体为四棱锥![]() ,下面部分几何体为四棱锥
,下面部分几何体为四棱锥![]() .
.
在平面![]() 中,过点
中,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 平面
平面![]() ,
,
所以![]() 是四棱锥
是四棱锥![]() 的高,
的高,
在![]() 中,因为
中,因为![]() ,所以
,所以![]() .
.
![]() 为直角梯形,其面积
为直角梯形,其面积![]()
![]() ,
,
所以四棱锥![]() 的体积
的体积![]()
![]() .
.
因三棱柱![]() 的体积
的体积![]()
![]() ,
,
所以下部分几何体![]() 的体积
的体积![]()
![]() ,
,
所以两部分几何体的体积之比为![]() .
.


科目:高中数学 来源: 题型:
【题目】今年入秋以来,某市多有雾霾天气,空气污染较为严重.市环保研究所对近期每天的空气污染情况进行调査研究后发现,每一天中空气污染指数与f(x)时刻x(时)的函数关系为f(x)=|log25(x+1)﹣a|+2a+1,x∈[0,24],其中a为空气治理调节参数,且a∈(0,1).
(1)若a= ![]() ,求一天中哪个时刻该市的空气污染指数最低;
,求一天中哪个时刻该市的空气污染指数最低;
(2)规定每天中f(x)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过3,则调节参数a应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区提倡低碳生活,环保出行,在小区提供自行车出租.该小区有40辆自行车供小区住户租赁使用,管理这些自行车的费用是每日92元,根据经验,若每辆自行车的日租金不超过5元,则自行车可以全部出租,若超过5元,则每超过1元,租不出的自行车就增加2辆,为了便于结算,每辆自行车的日租金x元只取整数,用f(x)元表示出租自行车的日纯收入(日纯收入=一日出租自行车的总收入﹣管理费用)
(1)求函数f(x)的解析式及其定义域;
(2)当租金定为多少时,才能使一天的纯收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() 的离心率e=
的离心率e= ![]() ,左顶点M到直线
,左顶点M到直线 ![]() =1的距离d=
=1的距离d= ![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A,B两点,若以AB为直径的圆经过坐标原点,证明:点O到直线AB的距离为定值;
(3)在(2)的条件下,试求△AOB的面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义运算为:a*b= ![]() ,如1*2=1,则函数f(x)=|2x*2﹣x﹣1|的值域为( )
,如1*2=1,则函数f(x)=|2x*2﹣x﹣1|的值域为( )
A.[0,1]
B.[0,1)
C.[0,+∞)
D.[1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com