
����Ŀ��ijС���ᳫ��̼����������У���С���ṩ���г����⣮��С����40�����г���С��ס������ʹ�ã�������Щ���г��ķ�����ÿ��92Ԫ�����ݾ��飬��ÿ�����г����������5Ԫ�������г�����ȫ�����⣬������5Ԫ����ÿ����1Ԫ���ⲻ�������г�������2����Ϊ�˱��ڽ��㣬ÿ�����г��������xԪֻȡ��������f��x��Ԫ��ʾ�������г����մ����루�մ�����=һ�ճ������г��������멁�������ã�
��1������f��x���Ľ���ʽ���䶨����
��2�������Ϊ����ʱ������ʹһ��Ĵ��������
���𰸡�
��1���⣺�����⣺��0��x��5��x��N*ʱ��f��x��=40x��92
��x��5��x��N*ʱ��f��x��=[40��2��x��5��]x��92=��2x2+50x��92
�� ![]()
�䶨����Ϊ{x|x��N*��x��40}
��2���⣺��0��x��5��x��N*ʱ��f��x��=40x��92��
�൱x=5ʱ��f��x��max=108��Ԫ��
��x��5��x��N*ʱ��f��x��=��2x2+50x��92=��2��x�� ![]() ��2+
��2+ ![]()
�߿������£��Գ���Ϊx= ![]() ��
��
�֡�x��N*���൱x=12��13ʱf��x��max=220��Ԫ��
��220��108���൱���Ϊ12Ԫ��13Ԫʱ��һ��Ĵ��������Ϊ220Ԫ
����������1�����ú�����ϵ��������ȡֵ��Χ�ڵľ������������Ĺ�ϵʽ��д���÷ֶκ������ǽ������Ĺؼ���ע��ʵ�������е��Ա���ȡֵ��Χ����2������һ�κ��������κ����ĵ����Խ������ֵ�����ǽ������Ĺؼ���ע���Ա���ȡֵ�����ϵĺ������ͣ�Ӧȡÿ�������ֵ�Ľϴ�ļ�Ϊ�ú��������ֵ��


 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ![]() ��������Բ
��������Բ![]() ��
�� ![]() ��
��![]() �������ֱ��
�������ֱ��![]() ��
��![]() ��
��![]() ������
������ ![]() Ϊ
Ϊ![]() ���е�����
���е�����![]() ��б��Ϊ9.
��б��Ϊ9.
������![]() �ķ�����
�ķ�����
����![]() ��
��![]() �������Ҷ�����
�������Ҷ����� ![]() ��
��![]() �ϵ����㣬��
�ϵ����㣬��![]() �����ı���
�����ı���![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2+4ax+2a+6��
��1��������f��x��=log2 f��x������СֵΪ2����a��ֵ��
��2����������x��R������f��x����0����������g��a��=2��a|a+3|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ǿռ���A�е�Ԫ�ظ����ã�A����ʾ�����壨A��B��= ![]() ����A={��1��0}��B={x||x2��2x��3|=a}���ң�A��B����1����a�����п���ֵΪ�� ��
����A={��1��0}��B={x||x2��2x��3|=a}���ң�A��B����1����a�����п���ֵΪ�� ��
A.{a|a��4}
B.{a|a��4��a=0}
C.{a|0��a��4}
D.{a|a��4��a=0}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�ĵ���ABCD�Ǿ��Σ�ƽ��PAB��ƽ��ABCD��PA=AB=3��BC=2��E��F�ֱ�����AD��PC���е� 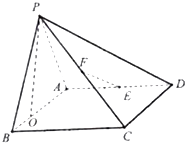
��1����֤��EF��ƽ��PBC
��2����ֱ��PC��ƽ��ABCD���ɽ�Ϊ ![]() ����P��AB�ϵ���ӰO�ڿ�����B��һ�࣬������P��EF��A������ֵ��
����P��AB�ϵ���ӰO�ڿ�����B��һ�࣬������P��EF��A������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
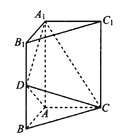
����Ŀ����ͼ��������![]() �У�����
������![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() ���е�.
���е�.
����֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
������ƽ��![]() �����������ֳɵ������ֵ����֮��.
�����������ֳɵ������ֵ����֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ��x+1��2+y2=25��Բ��ΪC��A��1��0����Բ��һ���㣬QΪԲ������һ�㣮�߶�AQ�Ĵ�ֱƽ������CQ�����߽��ڵ�M����M�Ĺ켣����Ϊ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ��U=R������y= ![]() +
+ ![]() �Ķ�����ΪA������y=
�Ķ�����ΪA������y= ![]() ��ֵ��ΪB��
��ֵ��ΪB��
��1����A��B��
��2����UA���ɣ�UB����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲM��x2+y2+4x��2y+3=0��ֱ��l����P����3��0����ԲM��Բ������������ֱ��l��ԲM���У���������y���ϵĽؾ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com