
【题目】设抛物线C:![]() 的焦点为F,抛物线上的点A到
的焦点为F,抛物线上的点A到![]() 轴的距离等于
轴的距离等于![]() .
.
(1)求抛物线C的方程;
(2)已知经过抛物线C的焦点F的直线![]() 与抛物线交于A,B两点,证明:
与抛物线交于A,B两点,证明: ![]() 为定值.
为定值.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)利用抛物线的性质和已知条件求出抛物线方程,进一步求得p值;
(2)分斜率存在与不存在两种情况,设过F的直线方程,与抛物线方程联立,整理后,设A(x1,y1),B(x2,y2)根据韦达定理可求得x1x2的值,又根据抛物线定义可知|AF|=x1+1,|BF|=x2+1代入![]() 可得其值.
可得其值.
(1)由题意可得,抛物线上点![]() 到焦点
到焦点![]() 的距离等于点
的距离等于点![]() 到直线
到直线![]() 的距离,由抛物线的定义得
的距离,由抛物线的定义得![]() ,即
,即![]() .故抛物线
.故抛物线![]() 的方程为
的方程为![]() ;
;
(2)易知焦点![]() 的坐标为
的坐标为![]() ,
,
若直线![]() 的斜率不存在,即直线
的斜率不存在,即直线![]() 方程为:
方程为:![]() ,此时
,此时![]() ,
,
![]() ,
,
若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 方程为:
方程为:![]() ,设
,设![]() ,
,
由抛物线的定义可知:![]() ,
,
由![]() 得:
得:![]() ,
,
由韦达定理得:![]() ,所以:
,所以:
![]() ,
,
综上可得:![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,若椭圆上一点
,若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]()
![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 轴的垂线,交椭圆
轴的垂线,交椭圆![]() 于
于![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以“你我中国梦,全民建小康”为主题、“社会主义核心价值观”为主线,为了了解![]() 两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对
两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对![]() 地区的100名观众进行统计,统计结果如下:
地区的100名观众进行统计,统计结果如下:
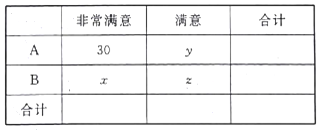
在被调查的全体观众中随机抽取1名“非常满意”的人是![]() 地区的概率为0.45,且
地区的概率为0.45,且![]() .
.
(Ⅰ)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“满意”的![]() 地区的人数各是多少?
地区的人数各是多少?
(Ⅱ)在(Ⅰ)抽取的“满意”的观众中,随机选出3人进行座谈,求至少有两名是![]() 地区观众的概率?
地区观众的概率?
(Ⅲ)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系?
的把握认为观众的满意程度与所在地区有关系?
附: 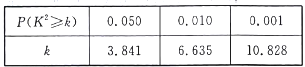 ,
, 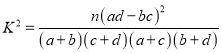 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,分别从两厂随机各选取了![]() 个轮胎,将每个轮胎的宽度(单位:
个轮胎,将每个轮胎的宽度(单位: ![]() )记录下来并绘制出如下的折线图:
)记录下来并绘制出如下的折线图:
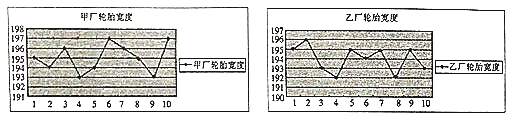
(1)分别计算甲、乙两厂提供的![]() 个轮胎宽度的平均值;
个轮胎宽度的平均值;
(2)轮胎的宽度在![]() 内,则称这个轮胎是标准轮胎.
内,则称这个轮胎是标准轮胎.
(i)若从甲乙提供的![]() 个轮胎中随机选取
个轮胎中随机选取![]() 个,求所选的轮胎是标准轮胎的概率
个,求所选的轮胎是标准轮胎的概率![]() ;
;
(ii)试比较甲、乙两厂分别提供的![]() 个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市“招手即停”公共汽车的票价按下列规则制定:5公里以内(含5公里),票价2元;5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).如果某条线路的总里程为20公里,
(1)请根据题意,写出票价![]() 与里程
与里程![]() 之间的函数解析式,并画出函数
之间的函数解析式,并画出函数![]() 的图象.
的图象.
(2)![]() 与
与![]() 在(5,10]内有且仅有1个公共点,求a范围.
在(5,10]内有且仅有1个公共点,求a范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com