
【题目】在△ABC中,角A,B,C所对的边分别是a,b,c,且![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,求
,求![]() .
.
【答案】(Ⅰ)证明详见解析;(Ⅱ)4.
【解析】试题分析:(Ⅰ)将已知等式通分后利用两角和的正弦函数公式整理,利用正弦定理,即可证明.(Ⅱ)由余弦定理求出A的余弦函数值,利用(Ⅰ)的条件,求解B的正切函数值即可
试题解析:(1)根据正弦定理,设![]() =
=![]() =
=![]() =k(k>0).
=k(k>0).
则a="ksin" A,b="ksin" B,c="ksin" C.
代入![]() +
+![]() =
=![]() 中,有
中,有![]() +
+![]() =
=![]() ,变形可得
,变形可得
sin Asin B="sin" Acos B+cos Asin B=sin(A+B).
在△ABC中,由A+B+C=π,有sin(A+B)=sin(π–C)="sin" C,
所以sin Asin B="sin" C.
(2)由已知,b2+c2–a2=![]() bc,根据余弦定理,有cos A=
bc,根据余弦定理,有cos A=![]() =
=![]() .
.
所以sin A=![]() =
=![]() .
.
由(Ⅰ),sin Asin B="sin" Acos B+cos Asin B,所以![]() sin B=
sin B=![]() cos B+
cos B+![]() sin B,
sin B,
故tan B=![]() =4.
=4.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】设定义域为R的奇函数 ![]() (a为实数). (Ⅰ)求a的值;
(a为实数). (Ⅰ)求a的值;
(Ⅱ)判断f(x)的单调性(不必证明),并求出f(x)的值域;
(Ⅲ)若对任意的x∈[1,4],不等式f(k﹣ ![]() )+f(2﹣x)>0恒成立,求实数k的取值范围.
)+f(2﹣x)>0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆的一个顶点坐标为(0,1),其离心率为 ![]()
(1)求椭圆的标准方程;
(2)椭圆上一点P满足∠F1PF2=60°,其中F1 , F2为椭圆的左右焦点,求△F1PF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A.茎叶图
B.分层抽样
C.独立性检验
D.回归直线方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程:x2+y2﹣2x﹣4y+m=0,其中m<5.
(1)若圆C与直线l:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(2)在(1)条件下,是否存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围,若不存在,说明理由.
,若存在,求出c的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图.
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据: ![]() yi=9.32,
yi=9.32, ![]() tiyi=40.17,
tiyi=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:相关系数r= 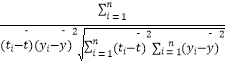 =
= 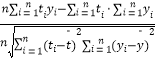
回归方程 ![]() =
= ![]() +
+ ![]() t中斜率和截距的最小二乘估计公式分别为:
t中斜率和截距的最小二乘估计公式分别为: ![]() =
= 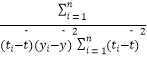 ,
, ![]() =
= ![]() ﹣
﹣ ![]() t.
t.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com