
����Ŀ����ͼ���ҹ�2009����2015������������������������λ���ڶ֣�������ͼ.
����������ͼ�������������Իع�ģ�����y��t�Ĺ�ϵ���������ϵ������˵����
������y����t�Ļع鷽�̣�ϵ����ȷ��0.01����Ԥ��2017���ҹ���������������������
�ο����ݣ� ![]() yi=9.32��
yi=9.32�� ![]() tiyi=40.17��
tiyi=40.17�� ![]() =0.55��
=0.55�� ![]() ��2.646��
��2.646��
�ο���ʽ�����ϵ��r= 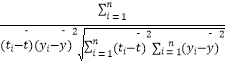 =
= 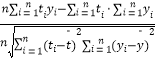
�ع鷽�� ![]() =
= ![]() +
+ ![]() t��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
t��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ�� ![]() =
= 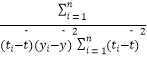 ��
�� ![]() =
= ![]() ��
�� ![]() t��
t��
���𰸡��⣺������y��t�����ϵ��r= ![]() ��0.99�� �ʿ������Իع�ģ����ϱ���y��t�Ĺ�ϵ��
��0.99�� �ʿ������Իع�ģ����ϱ���y��t�Ĺ�ϵ��
���� ![]() =4��
=4�� ![]() =
= ![]()
![]() yi �� ����
yi �� ���� ![]() =
=  =0.1��
=0.1��![]() =
= ![]() ��
�� ![]() t=
t= ![]() ��
��
�������Իع鷽��Ϊ ![]() =0.1t+0.93��
=0.1t+0.93��
��t=9ʱ�� ![]() =0.1��9+0.93=1.83��
=0.1��9+0.93=1.83��
��ˣ����ǿ���Ԥ��2017���ҹ�����������������1.83�ڶ�
�������������������y��t�����ϵ�����ɵý��ۣ���������ع�ϵ�����ɵûع鷽�̣�����Ԥ��2017���ҹ�����������������1.83�ڶ֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��������![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
��������![]() ��
��![]() ʱ��֤����
ʱ��֤����![]() ������
������![]() Ϊ��Ȼ�����ĵ�����.
Ϊ��Ȼ�����ĵ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���A,B,C���Եı߷ֱ���a,b,c,��![]() .
.
������֤����![]() ��
��
��������![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=loga��x+2����1��a��0��a��1����ͼ��������A������A��ֱ��mx+ny+1=0�ϣ�����m��0��n��0���� ![]() +
+ ![]() ����СֵΪ�� ��
����СֵΪ�� ��
A.3+2 ![]()
B.3+2 ![]()
C.7
D.11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=sin����x+�գ����أ�0��|��|�� ![]() ����ͼ����ͼ��ʾ��Ϊ�˵õ�g��x��=sin��x��ͼ����ֻҪ��f��x����ͼ�� ��
����ͼ����ͼ��ʾ��Ϊ�˵õ�g��x��=sin��x��ͼ����ֻҪ��f��x����ͼ�� �� 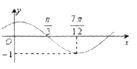
A.����ƽ�� ![]() ����λ����
�������
B.����ƽ�� ![]() ����λ����
�������
C.����ƽ�� ![]() ����λ����
�������
D.����ƽ�� ![]() ����λ����
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=8x�Ľ���ΪF����F����б��Ϊ60���ֱ��l��
��1����ֱ��l�ķ��̣�
��2����ֱ��l��������C���صõ��ҳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}������Ϊ�����ĵȲ����У�a1a2=3��a2a3=15��
��1��������{an}��ͨ�ʽ��
��2����bn=��an+1��2 ![]() ��������{bn}��ǰn���Tn ��
��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() �������ύ��
�������ύ��![]() ����ͼ��.
����ͼ��.
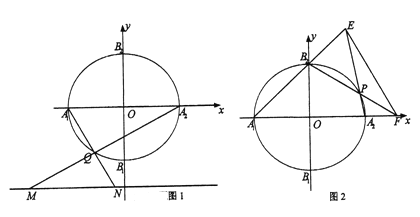
��1����![]() ��Բ
��Բ![]() �ϳ�
�ϳ�![]() �������㣨��ͼ1����
�������㣨��ͼ1����![]() ��ֱ��
��ֱ��![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ����
����![]() ����Сֵ��
����Сֵ��
��2����![]() ��Բ
��Բ![]() �ϳ�
�ϳ�![]() �������㣨��ͼ2����ֱ��
�������㣨��ͼ2����ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() .��
.��![]() ��б��Ϊ
��б��Ϊ![]() ��б��Ϊ
��б��Ϊ![]() ����֤��
����֤�� ![]() Ϊ��ֵ.
Ϊ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и��Ժ����У���ͬ���ǣ� ��
A.f��x��=lgx2 �� g��x��=2lgx
B.f��x��=lg ![]() ��g��x��=lg��x+1����lg��x��1��
��g��x��=lg��x+1����lg��x��1��
C.f��u��= ![]() ��g��v��=
��g��v��= ![]()
D.f��x��=x��g��x��= ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com