
 的正方体
的正方体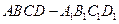 中,
中,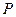 为线段
为线段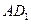 上的点,且满足
上的点,且满足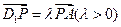 .
.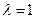 时,求证:平面
时,求证:平面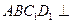 平面
平面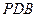 ;
;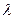 为何值,三棱锥
为何值,三棱锥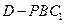 的体积
的体积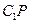 与
与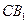 所成的角的余弦值.
所成的角的余弦值.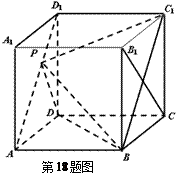 18.解:
18.解: 中,
中, 面
面 ,
,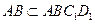 ∴平面
∴平面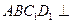 平面
平面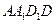 , ………………2分
, ………………2分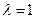 时,
时,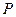 为
为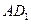 的中点,∴
的中点,∴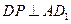 ,
,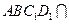 平面
平面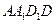
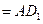 ,
,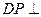 平面
平面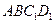 ,
,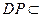 平面
平面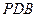 ,∴平面
,∴平面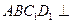 平面
平面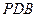 .………4分
.………4分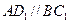 ,
,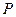 为线段
为线段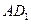 上的点,
上的点,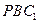 的面积为定值,即
的面积为定值,即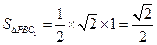 ,
,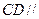 平面
平面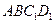 ,∴点
,∴点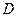 到平面
到平面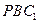 的距离为定值,即
的距离为定值,即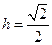 , ………………8分
, ………………8分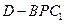 的体积为定值,即
的体积为定值,即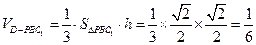 .
.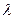 为何值,三棱锥
为何值,三棱锥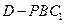 的体积恒为定值
的体积恒为定值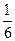 ;………………………10分
;………………………10分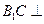 平面
平面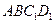 ,
,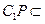 平面
平面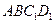 ,∴
,∴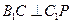 , …………………………12分
, …………………………12分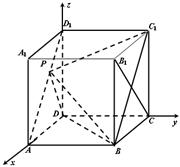 即异面直线
即异面直线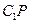 与
与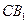 所成的角为定值
所成的角为定值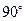 ,从而其余弦值为
,从而其余弦值为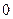 .…………………13分
.…………………13分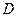 为坐标原点,建立如图所示的坐标系.
为坐标原点,建立如图所示的坐标系.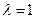 时,即点
时,即点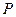 为线段
为线段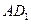 的中点,则
的中点,则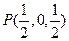 ,又
,又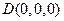 、
、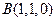
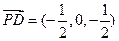 ,
,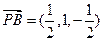 ,设平面
,设平面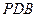 的法向量为
的法向量为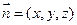 ,……1分
,……1分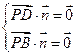 ,即
,即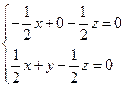 ,令
,令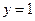 ,解得
,解得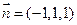 , …2分
, …2分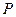 为线段
为线段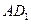 的中点,∴
的中点,∴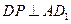 ,∴
,∴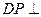 平面
平面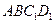 ,
,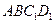 的法向量为
的法向量为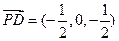 , ……………3分
, ……………3分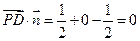 ,
,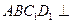 平面
平面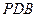 , ………………………4分
, ………………………4分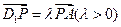 ,∴
,∴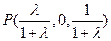 , …………………10分
, …………………10分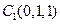 、
、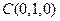 、
、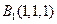 ,
,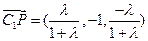 ,
,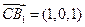 , ……………………………11分
, ……………………………11分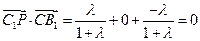 …………………………………12分
…………………………………12分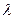 取值多少,都有
取值多少,都有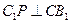 ,即异面直线
,即异面直线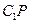 与
与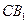 所成的角的余弦值为0.……13分
所成的角的余弦值为0.……13分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 B=1,BC=a,PA⊥平面ABCD
B=1,BC=a,PA⊥平面ABCD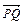 ⊥
⊥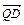 ,说明理由.
,说明理由.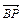 ,
,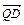 >=
>=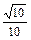 时,求点P的位置.
时,求点P的位置.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
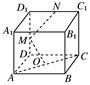
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
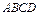 所在的平面与平面
所在的平面与平面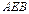 垂直,且
垂直,且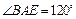 ,
,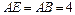 ,
,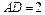 ,
,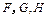 分别为
分别为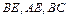 的中点.
的中点.
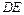 与平面
与平面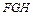 平行;
平行;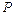 在直线
在直线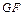 上,且二面角
上,且二面角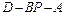 的大小为
的大小为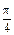 ,试确定点
,试确定点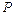 的位置.
的位置.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
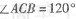 ,SC=AC=BC=
,SC=AC=BC=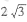 ,M为SB中点,N在AB上,满足MN 丄 BC.
,M为SB中点,N在AB上,满足MN 丄 BC.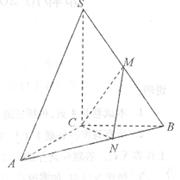
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.16 | B.24或 |
| C.14 | D.20 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
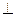 底面ABCD,PD=AD
底面ABCD,PD=AD
 平面PBD
平面PBD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com