练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用1、2、3、4、5、6组成六位数(没有重复数字)，要求任何相邻两个数字的奇偶性不同，且1和2相邻，这样的六位数的个数是________．(用数字作答)


    40

    解析：由题先排除1和2的剩余4个元素有2A·A＝8种方案，再向这排好的4个元素中插入1和2捆绑的整体，有A种插法，∴ 不同的安排方案共有2A·A·A＝40种．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设变量x、y满足约束条件：则z＝x－3y的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    (1) 若a>b>c，求证：

    (2) 若a>b>c，求使得恒成立的k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个口袋内有4个不同的红球，6个不同的白球．

    (1) 从中任取4个球，红球的个数不比白球少的取法有多少种？

    (2) 若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    规定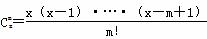，其中x∈R，m是正整数，且C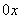＝1这是组合数C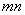(n、m是正整数，且m≤n)的一种推广．

    (1)  求C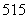的值；

    (2) 组合数的两个性质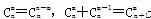：是否都能推广到C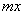(x∈R，m∈N*)的情形？若能推广，则写出推广的形式并给予证明；若不能，则说明理由；

    (3) 已知组合数C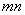是正整数，求证：当x∈Z，m是正整数时，C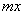∈Z.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    书架上层放有6本不同的数学书，下层放有5本不同的语文书，从中任取数学书与语文书各一本，有________种不同的取法．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用三种不同的颜色填涂下图3×3方格中的9个区域，要求每行、每列的三个区域都不同色，则不同的填涂方法共有________种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若(1＋x)n的展开式中，x3的系数是x的系数的7倍，求n；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有一种闯三关游戏规则规定如下：用抛掷正四面体型骰子(各面上分别有1，2，3，4点数的质地均匀的正四面体)决定是否过关，在闯第n(n＝1，2，3)关时，需要抛掷n次骰子，当n次骰子面朝下的点数之和大于n2时，则算闯此关成功，并且继续闯关，否则停止闯关．每次抛掷骰子相互独立．

    (1)  求仅闯过第一关的概率；

    (2)  记成功闯过的关数为ξ，求ξ的分布列．

    查看答案和解析>>

    同步练习册答案