练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    有一种闯三关游戏规则规定如下：用抛掷正四面体型骰子(各面上分别有1，2，3，4点数的质地均匀的正四面体)决定是否过关，在闯第n(n＝1，2，3)关时，需要抛掷n次骰子，当n次骰子面朝下的点数之和大于n2时，则算闯此关成功，并且继续闯关，否则停止闯关．每次抛掷骰子相互独立．

    (1)  求仅闯过第一关的概率；

    (2)  记成功闯过的关数为ξ，求ξ的分布列．


    解：(1) 记“仅闯过第一关的概率”这一事件为A，则P(A)＝·＝.

    (2) 由题意得，ξ的取值有0，1，2，3，且P(ξ＝0)＝，P(ξ＝1)＝，P(ξ＝2)＝··＝，P(ξ＝3)＝··＝，即随机变量ξ的概率分布列为

    ξ

    0

    1

    2

    3

    P

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    用1、2、3、4、5、6组成六位数(没有重复数字)，要求任何相邻两个数字的奇偶性不同，且1和2相邻，这样的六位数的个数是________．(用数字作答)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    0.9915的近似值是___________．(精确到0.001)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现在某类病毒记作XmYn，其中正整数m，n(m≤7，n≤9)可以任意选取，则m，n都取到奇数的概率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某人射击一次击中目标的概率为0.6，经过3次射击，此人恰有两次击中目标的概率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为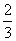，中奖可以获得2分；方案乙的中奖率为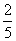，中奖可以得3分；未中奖则不得分．每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品．

    若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X，求X≤3的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     电视台综艺频道组织的闯关游戏，游戏规定前两关至少过一关才有资格闯第三关，闯关者闯第一关成功得3分，闯第二关成功得3分，闯第三关成功得4分．现有一位参加游戏者单独闯第一关、第二关、第三关成功的概率分别为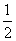、、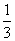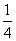，记该参加者闯三关所得总分为ξ.

    (1) 求该参加者有资格闯第三关的概率；

    (2) 求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为防止山体滑坡，某地决定建设既美化又防护的绿化带，种植松树、柳树等植物．某人一次种植了n株柳树，各株柳树成活与否是相互独立的，成活率为p，设ξ为成活柳树的株数，数学期望E(ξ)＝3，标准差σ(ξ)为.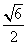

    (1) 求n、p的值并写出ξ的分布列；

    (2) 若有3株或3株以上的柳树未成活，则需要补种，求需要补种柳树的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     正四面体ABCD的体积为V，P是正四面体ABCD的内部的一个点．

    (1) 设“VPABC≥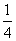V”的事件为X，求概率P(X)；

    (2) 设“VPABC≥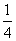V”且“VPBCD≥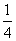V”的事件为Y，求概率P(Y)．

    查看答案和解析>>

    同步练习册答案