
规定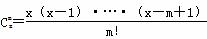 ,其中x∈R,m是正整数,且C
,其中x∈R,m是正整数,且C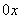 =1这是组合数C
=1这是组合数C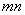 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.
(1) 求C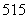 的值;
的值;
(2) 组合数的两个性质: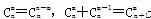 是否都能推广到C
是否都能推广到C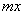 (x∈R,m∈N*)的情形?若能推广,则写出推广的形式并给予证明;若不能,则说明理由;
(x∈R,m∈N*)的情形?若能推广,则写出推广的形式并给予证明;若不能,则说明理由;
(3) 已知组合数C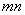 是正整数,求证:当x∈Z,m是正整数时,C
是正整数,求证:当x∈Z,m是正整数时,C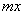 ∈Z.
∈Z.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
某商场若将进货单价为8元的商品按每件10元出售,每天可销售100件,现准备采用提高售价,减少进货量的办法来增加利润,已知这种商品每件销售价提高1元,销售量就要减少10件,问该商场将销售价每件定为多少元时,才能使得每天所赚的利润最多?销售价每件定为多少元时,才能保证每天所赚的利润在300元以上?
查看答案和解析>>
科目:高中数学 来源: 题型:
用1、2、3、4、5、6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2相邻,这样的六位数的个数是________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通,从丁地到丙地有2条路可通.则从甲地到丙地共有________种不同的走法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com