
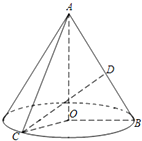
 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.分析 (1)求出圆锥底面半径,圆锥的侧面积S侧,然后求解圆锥的全面积.
(2)过D作DM∥AO交BO于M,连CM,说明∠CDM为异面直线AO与CD所成角,在Rt△CDM中,求解异面直线AO与CD所成角的大小.
解答 解:(1)Rt△AOB中,OB=2
即圆锥底面半径为2
圆锥的侧面积S侧=πrl=8π….4’
故圆锥的全面积S全=S侧+S底=8π+4π=12π….6’
(2)过D作DM∥AO交BO于M,连CM
则∠CDM为异面直线AO与CD所成角….8’
∵AO⊥平面OBC∴DM⊥平面OBC∴DM⊥MC
在Rt△AOB中,$AO=2\sqrt{3}$∴$DM=\sqrt{3}$,
∵D是AB的中点∴M是OB的中点,
∴OM=1∴$CM=\sqrt{5}$.
在Rt△CDM中,$tan∠CDM=\frac{{\sqrt{5}}}{{\sqrt{3}}}=\frac{{\sqrt{15}}}{3}$,….10’
∴$∠CDM=arctan\frac{{\sqrt{15}}}{3}$,
即异面直线AO与CD所成角的大小为$arctan\frac{{\sqrt{15}}}{3}$….12’
点评 本题考查异面直线所成角的求法,几何体的全面积的求法,考查空间想象能力以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
 在正方体ABCD-A1B1C1D1中,已知M,N分别是A1B1,BB1的中点,过M,N,C1的截面截正方体所得的几何体,如图所示,那么该几何体的侧视图是( )
在正方体ABCD-A1B1C1D1中,已知M,N分别是A1B1,BB1的中点,过M,N,C1的截面截正方体所得的几何体,如图所示,那么该几何体的侧视图是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在执行程序框图所示的算法时,若输入a3,a2,a1,a0的值依次是1,-3,3,-1,则输出v的值为( )
如图,在执行程序框图所示的算法时,若输入a3,a2,a1,a0的值依次是1,-3,3,-1,则输出v的值为( )| A. | -2 | B. | 2 | C. | -8 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2) | B. | [1,5) | C. | [1,2) | D. | [-2,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com