
分析 (Ⅰ)根据向量减法的几何意义,在$\overrightarrow{OC}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}$两边同减去$\overrightarrow{OA}$,进行向量的数乘运算便可得出$\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AB}$,这样便可得出三点A,B,C共线;
(Ⅱ)根据上面容易求出点C的坐标,并求出向量$\overrightarrow{AB}$的坐标,从而得出f(x)=(cosx-m)2+1-m2,这样根据配方的式子,讨论m的取值:m<0,0≤m≤1,m>1,这样即可求出m的值.
解答 解:(Ⅰ)由已知得$\overrightarrow{OC}-\overrightarrow{OA}=\frac{2}{3}(\overrightarrow{OB}-\overrightarrow{OA})$;
即$\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AB}$;
∴$\overrightarrow{AC}∥\overrightarrow{AB}$,又∵$\overrightarrow{AC},\overrightarrow{AB}$有公共点A;
∴A,B,C三点共线;
(Ⅱ)$\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AB}$;
∴$C(1+\frac{2}{3}cosx,cosx)$;
∵$\overrightarrow{AB}=(cosx,0)$;
∴$f(x)=\overrightarrow{OA}•\overrightarrow{OC}-(2m+\frac{2}{3})•|\overrightarrow{AB}|$
=$1+\frac{2}{3}cosx+co{s}^{2}x-(2m+\frac{2}{3})cosx$
=(cosx-m)2+1-m2;
∵$x∈[0,\frac{π}{2}]$,∴cosx∈[0,1];
①当m<0,当且仅当cosx=0时,f(x)取得最小值为1(舍去)
②当0≤m≤1时,当且仅当cosx=m时,f(x)取得最小值为1-m2,$m=±\frac{\sqrt{10}}{2}$(舍去)
③当m>1时,当且仅当cosx=1时,f(x)取得最小值2-2m,2-2m=$-\frac{3}{2}$;
∴$m=\frac{7}{4}$
综上m=$\frac{7}{4}$.
点评 考查向量减法的几何意义,向量的数乘运算,以及共线向量基本定理,根据点的坐标求向量的坐标,以及配方求二次函数最值的方法.


科目:高中数学 来源: 题型:选择题
| A. | 5000 | B. | 4950 | C. | 99 | D. | $\frac{99}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\sqrt{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{3}x$ | C. | $y=±\sqrt{2}x$ | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
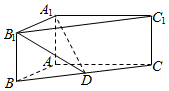 如图,在直三棱柱ABC-A1B1C1中,AB=2$\sqrt{2}$,AC=2$\sqrt{3}$,AA1=1,∠BAC=90°,D为线段BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=2$\sqrt{2}$,AC=2$\sqrt{3}$,AA1=1,∠BAC=90°,D为线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图是一个几何体的三视图,正视图是边长为2的正三角形,俯视图是等腰直角三角形,该几何体的表面积为$4+\sqrt{3}+\sqrt{7}$,体积为$\frac{{2\sqrt{3}}}{3}$.
如图是一个几何体的三视图,正视图是边长为2的正三角形,俯视图是等腰直角三角形,该几何体的表面积为$4+\sqrt{3}+\sqrt{7}$,体积为$\frac{{2\sqrt{3}}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com