
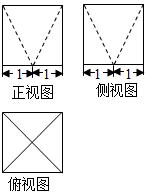
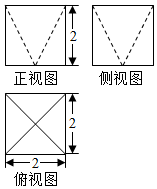
 如图是一个几何体的三视图,正视图是边长为2的正三角形,俯视图是等腰直角三角形,该几何体的表面积为$4+\sqrt{3}+\sqrt{7}$,体积为$\frac{{2\sqrt{3}}}{3}$.
如图是一个几何体的三视图,正视图是边长为2的正三角形,俯视图是等腰直角三角形,该几何体的表面积为$4+\sqrt{3}+\sqrt{7}$,体积为$\frac{{2\sqrt{3}}}{3}$. 分析 由三视图可知:该几何体为一个三棱锥P-ABC,底面△ABC是等腰直角三角形,△PBC是边长为2的正三角形,且平面PBC⊥底面ABC.利用三角形面积计算公式、三棱锥的体积计算公式即可得出.
解答 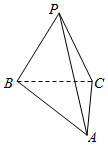 解:由三视图可知:该几何体为一个三棱锥P-ABC,底面△ABC是等腰直角三角形,
解:由三视图可知:该几何体为一个三棱锥P-ABC,底面△ABC是等腰直角三角形,
△PBC是边长为2的正三角形,且平面PBC⊥底面ABC.
∴该几何体的表面积为=$\frac{\sqrt{3}}{4}×{2}^{2}$+$\frac{1}{2}×2×2$+$\frac{1}{2}×2×2$+$\frac{1}{2}×2\sqrt{2}$×$\sqrt{(\sqrt{3})^{2}+(\frac{\sqrt{2}}{2})^{2}}$
=4+$\sqrt{3}$+$\sqrt{7}$,
体积V=$\frac{1}{3}×\frac{1}{2}×{2}^{2}×\sqrt{3}$=$\frac{2\sqrt{3}}{3}$.
故答案分别为:4+$\sqrt{3}$+$\sqrt{7}$;$\frac{2\sqrt{3}}{3}$.
点评 本题考查了三视图的有关计算、三棱锥的体积与表面积计算公式,考查了推理能力与计算能力,属于中档题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
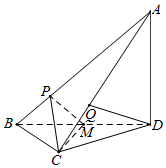 如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.
如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
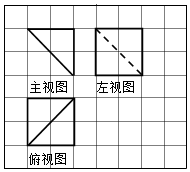
| A. | $\frac{2\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{9π}$ | C. | $\frac{\sqrt{2}}{16π}$ | D. | $\frac{8\sqrt{2}}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 工作 效益 机器 | 一 | 二 | 三 | 四 | 五 |
| 甲 | 15 | 17 | 14 | 17 | 15 |
| 乙 | 22 | 23 | 21 | 20 | 20 |
| 丙 | 9 | 13 | 14 | 12 | 10 |
| 丁 | 7 | 9 | 11 | 9 | 11 |
| 戊 | 13 | 15 | 14 | 15 | 11 |
| A. | 甲只能承担第四项工作 | B. | 乙不能承担第二项工作 | ||
| C. | 丙可以不承担第三项工作 | D. | 获得的效益值总和为78 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4cm3 | B. | 8cm3 | C. | $\frac{16}{3}$cm3 | D. | $\frac{32}{3}$cm3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com