
分析 可求导数得到$f′(x)=\frac{4(1-{x}^{2})}{({x}^{2}+1)^{2}}$,这样便可得出函数f(x)的单调递增区间,而由条件函数f(x)在区间[m,m+1]上单调递增便可得出关于m的不等式组,从而求出实数m的取值范围.
解答 解:$f′(x)=\frac{4({x}^{2}+1)-8{x}^{2}}{({x}^{2}+1)^{2}}=\frac{4(1-{x}^{2})}{({x}^{2}+1)^{2}}$;
∴-1≤x≤1时,f′(x)≥0;
即区间[-1,1]是f(x)的单调递增区间;
又f(x)在[m,m+1]上是单调递增函数;
∴$\left\{\begin{array}{l}{m≥-1}\\{m+1≤1}\end{array}\right.$;
∴-1≤m≤0;
即实数m的取值范围是[-1,0].
故答案为:[-1,0].
点评 考查商的导数的计算公式,用导数求函数单调区间的方法,一元二次不等式的解法,以及区间的概念及数轴表示区间的方法.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$-$\frac{2}{5}$i | B. | -$\frac{2}{5}$-$\frac{1}{5}$i | C. | $\frac{1}{5}$+$\frac{2}{5}$i | D. | $\frac{2}{5}$+$\frac{1}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{C}_{7}^{4}{•C}_{9}^{6}}{{C}_{16}^{10}}$ | B. | $\frac{{C}_{10}^{4}{•C}_{10}^{6}}{{C}_{16}^{10}}$ | ||
| C. | $\frac{{C}_{7}^{4}{•C}_{9}^{6}}{{C}_{16}^{7}}$ | D. | $\frac{{C}_{16}^{7}{•C}_{16}^{3}}{{C}_{16}^{10}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
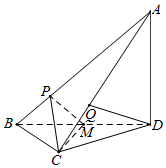 如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.
如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com