
| A. | 6 | B. | -6 | C. | -3 | D. | 2 |
分析 可画出图形,根据条件即可得到$\overrightarrow{AB}=2\overrightarrow{DC},∠D=120°$,根据向量减法几何意义即可得到$\overrightarrow{AC}=\overrightarrow{DC}-\overrightarrow{DA},\overrightarrow{BD}=-2\overrightarrow{DC}-\overrightarrow{DA}$,从而由向量的数量积的运算即可得出$\overrightarrow{AC}•\overrightarrow{BD}$的值.
解答 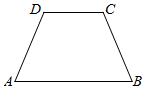 解:如图,根据条件,AB=4,$\overrightarrow{AB}=2\overrightarrow{DC}$,∠D=120°;$\overrightarrow{AC}=\overrightarrow{DC}-\overrightarrow{DA}$,$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$=$-2\overrightarrow{DC}-\overrightarrow{DA}$;
解:如图,根据条件,AB=4,$\overrightarrow{AB}=2\overrightarrow{DC}$,∠D=120°;$\overrightarrow{AC}=\overrightarrow{DC}-\overrightarrow{DA}$,$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$=$-2\overrightarrow{DC}-\overrightarrow{DA}$;
∴$\overrightarrow{AC}•\overrightarrow{BD}=(\overrightarrow{DC}-\overrightarrow{DA})•(-2\overrightarrow{DC}-\overrightarrow{DA})$
=$-2{\overrightarrow{DC}}^{2}+\overrightarrow{DC}•\overrightarrow{DA}+{\overrightarrow{DA}}^{2}$
=-8-2+4
=-6.
故选B.
点评 考查等腰梯形的定义,向量减法的几何意义,以及向量的数乘运算,向量的数量积的运算及计算公式.


科目:高中数学 来源: 题型:选择题
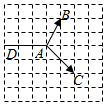
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{5}{2}$ | D. | $-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,其中俯视图中的弧线是半径为1的四分之一个圆弧,则该几何体的体积为( )
某几何体的三视图如图所示,其中俯视图中的弧线是半径为1的四分之一个圆弧,则该几何体的体积为( )| A. | 1 | B. | 2π | C. | 1-$\frac{π}{4}$ | D. | 1-$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
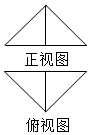 把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C-ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C-ABD的表面积为4+2$\sqrt{3}$.
把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C-ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C-ABD的表面积为4+2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\sqrt{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{3}x$ | C. | $y=±\sqrt{2}x$ | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知平行四边形ABCD中,∠A=45°,且AB=BD=1,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示:
已知平行四边形ABCD中,∠A=45°,且AB=BD=1,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com