
分析 (Ⅰ)利用复数相等与代数运算,列出方程求出k的值;
(Ⅱ)写出直线l的方程,求出直线l与曲线y=$\sqrt{x}$的交点,再利用积分求对应的面积.
解答 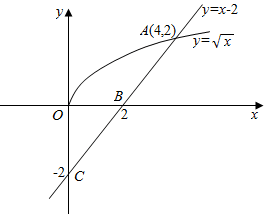 解:(Ⅰ)复数z=k-2i的共轭复数$\overline{z}$=k+2i,
解:(Ⅰ)复数z=k-2i的共轭复数$\overline{z}$=k+2i,
且z-($\frac{1}{2}$-i)=$\frac{\overline{z}}{2}$-2i,
∴(k-2i)-($\frac{1}{2}$-i)=$\frac{1}{2}$(k+2i)-2i,
∴(k-$\frac{1}{2}$)-i=$\frac{1}{2}$k-i,
即k-$\frac{1}{2}$=$\frac{1}{2}$k,
解得k=1;
(Ⅱ)过点(0,-2)的直线l的斜率为k=1,
∴直线l的方程为:y=x-2;
令$\left\{\begin{array}{l}{y=x-2}\\{y=\sqrt{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,
∴直线l与曲线y=$\sqrt{x}$的交点为(4,2);
如图所示
曲线y=$\sqrt{x}$与直线y=x-2以及y轴所围成的图形的面积为:
S△OBC+∫02$\sqrt{x}$dx+∫24($\sqrt{x}$-x+2)dx=$\frac{1}{2}$×2×2+$\frac{2}{3}$${x}^{\frac{3}{2}}$${|}_{0}^{2}$+($\frac{2}{3}$${x}^{\frac{3}{2}}$-$\frac{1}{2}$x2+2x)${|}_{2}^{4}$=$\frac{16}{3}$.
点评 本题考查了复数的代数运算问题,也考查了用定积分求面积的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$-$\frac{2}{5}$i | B. | -$\frac{2}{5}$-$\frac{1}{5}$i | C. | $\frac{1}{5}$+$\frac{2}{5}$i | D. | $\frac{2}{5}$+$\frac{1}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{5\sqrt{2}}}{13}$ | B. | $\frac{{7\sqrt{2}}}{13}$ | C. | $\frac{{17\sqrt{2}}}{26}$ | D. | $\frac{{7\sqrt{2}}}{26}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AB∥CD,AB⊥AD,AB=2AD=2AP=2CD=2,E是棱PC上一点,且CE=2PE.
如图所示,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AB∥CD,AB⊥AD,AB=2AD=2AP=2CD=2,E是棱PC上一点,且CE=2PE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com