
分析 (Ⅰ)令x=1,则$(x+\frac{1}{x}){(3x-\frac{1}{x})^n}$展开式中各项系数和为2n+1=64,解出n即可得出.
(Ⅱ)由(Ⅰ)知,$(x+\frac{1}{x}){(3x-\frac{1}{x})^n}$=$(x+\frac{1}{x}){(3x-\frac{1}{x})^5}$,要求展开式的常数项,只需求${(3x-\frac{1}{x})^5}$展开式中含$x和\frac{1}{x}$的项,利用通项公式即可得出.
解答 解:(Ⅰ)令x=1,则$(x+\frac{1}{x}){(3x-\frac{1}{x})^n}$展开式中各项系数和为2n+1=64,
解得:n=5.
(Ⅱ)由(Ⅰ)知,$(x+\frac{1}{x}){(3x-\frac{1}{x})^n}$=$(x+\frac{1}{x}){(3x-\frac{1}{x})^5}$,
要求展开式的常数项,只需求${(3x-\frac{1}{x})^5}$展开式中含$x和\frac{1}{x}$的项.
由通项公式得${T_{r+1}}=C_5^r{(3x)^{5-r}}{(-\frac{1}{x})^r}=C_5^r{3^{5-r}}{(-1)^r}{x^{5-2r}}$,
令5-2r=±1,得r=2或r=3.
所以该展开式中的常数项为$C_5^2{3^3}-C_5^3{3^2}=180$.
点评 本题主要考查二项展开式等基础知识,考查运算化简能力、推理计算能力、化归转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错 | B. | 小前提错 | ||
| C. | 推理形式错 | D. | 大前提和小前提都错 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 单价x(元) | 3 | 4 | 5 | 6 | 7 |
| 销量y(件) | 78 | 72 | 69 | 68 | 63 |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 30种 | C. | 96种 | D. | 144种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
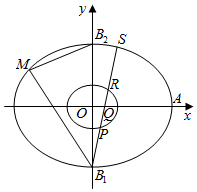 定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.
定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
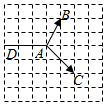
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{5}{2}$ | D. | $-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com