
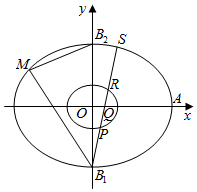
 定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.
定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.分析 (Ⅰ)(i)设C的方程:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),则$\left\{\begin{array}{l}{2b=6}\\{c=\sqrt{3}b}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,求出a,b,即可求C的方程;
(ii)求出轨迹C1,可得离心率相等,即可证明C1与C相似;
(Ⅱ)设直线方程为y=kx-3(k>0),代入椭圆方程,求出相应线段的长,可得$\frac{|{B}_{1}S{|}^{2}-|PR{|}^{2}}{|AQ|}$=$\frac{128k(1+{k}^{2})}{3(1+4{k}^{2})(2k-1)}$构造函数,利用导数确定函数的单调性,即可确定$\frac{|{B}_{1}S{|}^{2}-|PR{|}^{2}}{|AQ|}$的取值范围.
解答 (Ⅰ)(i)解:设C的方程:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),则$\left\{\begin{array}{l}{2b=6}\\{c=\sqrt{3}b}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,
∴a=6,b=3,
∴C的方程:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{9}$=1;
(ii)证明:设G(x,y),M(x0,y)(x0≠0),则x0=3x,y0=3y
把点M(3x,3y)的坐标代入C的方程,得轨迹C1的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1(x≠0),
∴轨迹C1也为椭圆(除去(0,-1),(0,1)两点),求得a1=2,c1=$\sqrt{3}$,e1=$\frac{\sqrt{3}}{2}$,
∵C的离心率e=$\frac{\sqrt{3}}{2}$,
∴e1=e,
∴C1与C相似;
(Ⅱ)解:设直线方程为y=kx-3(k>0),代入C的方程得(1+4k2)x2-24kx=0,∴xS=$\frac{24k}{1+4{k}^{2}}$,yS=$\frac{12{k}^{2}-3}{1+4{k}^{2}}$,
∴$|{B}_{1}S{|}^{2}$=$\frac{(24k)^{2}(1+{k}^{2})}{(1+4{k}^{2})^{2}}$,
代入C1的方程得(1+4k2)x2-24kx+32=0,由k>0,△>0得k>$\sqrt{2}$,
由韦达定理得xP+xR=$\frac{24k}{1+4{k}^{2}}$,xPxR=$\frac{32}{1+4{k}^{2}}$,
∴|PR|2=(1+k2)[$\frac{(24k)^{2}}{(1+4{k}^{2})^{2}}$-$\frac{128}{1+4{k}^{2}}$].
∵|AQ|=6-$\frac{3}{k}$=$\frac{3(2k-1)}{k}$,
∴$\frac{|{B}_{1}S{|}^{2}-|PR{|}^{2}}{|AQ|}$=$\frac{128k(1+{k}^{2})}{3(1+4{k}^{2})(2k-1)}$
令f(k)=$\frac{128k(1+{k}^{2})}{3(1+4{k}^{2})(2k-1)}$(k$>\sqrt{2}$)
则f′(k)=$\frac{1}{3}$•$\frac{128[4{k}^{4}+{k}^{2}(12k-1)+1]}{(8{k}^{3}-4{k}^{2}+2k-1)^{2}}$<0
∴f(k)在($\sqrt{2}$,+∞)上是减函数,
∴$f(k)<f(\sqrt{2}$)=$\frac{128(4+\sqrt{2})}{63}$
∴0<$\frac{|{B}_{1}S{|}^{2}-|PR{|}^{2}}{|AQ|}$<$\frac{128(4+\sqrt{2})}{63}$.
点评 本题考查椭圆的方程与性质,考查直线与椭圆的位置关系,考查导数知识的运用,考查学生分析解决问题的能力,知识综合性强.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com