
分析 由题意,令f(x)=x2-2mx+m2-1,利用B={x|$\frac{1}{2}$<x<$\frac{2}{3}$},B?A,可得$\left\{\begin{array}{l}{f(\frac{1}{2})≤0}\\{f(\frac{2}{3})≤0}\end{array}\right.$,解不等式组,即可求实数m的取值范围.
解答 解:由题意,令f(x)=x2-2mx+m2-1,则
∵B={x|$\frac{1}{2}$<x<$\frac{2}{3}$},B?A,
∴$\left\{\begin{array}{l}{f(\frac{1}{2})≤0}\\{f(\frac{2}{3})≤0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{m}^{2}-m-\frac{3}{4}≤0}\\{{m}^{2}-\frac{4}{3}m-\frac{5}{9}≤0}\end{array}\right.$,
∴-$\frac{1}{2}$≤m≤$\frac{3}{2}$.
点评 本题考查集合的包含关系,考查函数思想的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 单价x(元) | 3 | 4 | 5 | 6 | 7 |
| 销量y(件) | 78 | 72 | 69 | 68 | 63 |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
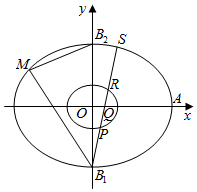 定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.
定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{5}{2}$ | D. | $-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com