
分析 (1)求得f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间,可得极大值,无极小值;
(2)由题意可得要证原不等式成立,令x=e+k2,可得原不等式即为xlnx>2x-e,即证x>e时,即xlnx-2x+e>0,令g(x)=xlnx-2x+e(x>e),求出导数,判断单调性,即可得证.
解答 解:(1)函数f(x)=$\frac{lnx-x}{x}$(x>0)的导数为f′(x)=$\frac{1-lnx}{{x}^{2}}$,
令$\frac{1-lnx}{{x}^{2}}$=0,可得x=e,
当x>e时,f′(x)<0;当0<x<e时,f′(x)>0.
可得f(x)的增区间为(0,e),减区间为(e,+∞);
f(x)的极大值为f(e)=$\frac{1-e}{e}$,无极小值;
(2)证明:要证原不等式成立,
令x=e+k2,可得原不等式即为xlnx>2x-e,
即证x>e时,xlnx>2x-e,
即xlnx-2x+e>0,
令g(x)=xlnx-2x+e(x>e),可得g′(x)=1+lnx-2=lnx-1,
当x>e时,g′(x)>0,g(x)递增;
即有g(x)>g(e)=elne-2e+e=0,
则x>e时,xlnx>2x-e成立,
即有对于任意的非零实数k,
不等式(e+k2)ln(e+k2)>e+2k2恒成立.
点评 本题考查导数的运用:求单调区间和极值、最值,考查不等式成立问题的解法,注意运用转化思想,构造函数法,判断单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在平行四边形OABC中,点E,F分别在AB,BC上,且满足AB=2AE,BC=3CF.若$\overrightarrow{OB}$=λ$\overrightarrow{OE}$+μ$\overrightarrow{OF}$(λ、μ∈R),则λ+μ=$\frac{7}{5}$.
如图,在平行四边形OABC中,点E,F分别在AB,BC上,且满足AB=2AE,BC=3CF.若$\overrightarrow{OB}$=λ$\overrightarrow{OE}$+μ$\overrightarrow{OF}$(λ、μ∈R),则λ+μ=$\frac{7}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
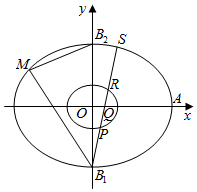 定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.
定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com