
| A. |  | B. |  | C. |  | D. | 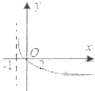 |
分析 先根据奇函数的定义求出b的值,再根据图象的平移即可得到答案.
解答 解:∵$f(x)=\frac{{{a^x}+1}}{{{a^x}-b}}(0<a<1)$$\frac{{a}^{-x}+1}{{a}^{-x}-b}$的图象关于原点对称,
∴f(-x)=-f(x)
∴$\frac{{a}^{-x}+1}{{a}^{-x}-b}$=$\frac{{a}^{x}+1}{1-b{a}^{x}}$=-$\frac{{a}^{x}+1}{b{a}^{x}-1}$=-$\frac{{a}^{x}+1}{{a}^{x}-b}$
即b=1,
g(x)=loga(x+b)=loga(x+1),
∴g(x)=loga(x+1)是由y=logax先左平移一个单位得到,
故选:D
点评 本题考查了奇函数的性质和对数函数的性质,属于基础题.


科目:高中数学 来源: 题型:填空题
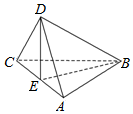 如图,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的有③(写出全部正确命题的序号).
如图,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的有③(写出全部正确命题的序号).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|3≤x<6} | B. | {x|3<x<6} | C. | {x|3<x≤6} | D. | {x|3≤x≤6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com