练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．若圆锥的侧面展开图圆心角为120°，则圆锥的底面半径和母线之比为$\frac{1}{3}$．

    分析 利用弧长公式，即可得出结论．

    解答 解：圆锥的侧面展开图圆心角为120°=$\frac{2π}{3}$，
    ∴2πr=$\frac{2π}{3}l$，
    ∴$\frac{r}{l}$=$\frac{1}{3}$．
    故答案为$\frac{1}{3}$．

    点评 本题考查弧长公式，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    1．在?ABCD中，$\overrightarrow{AD}$=（3，7），$\overrightarrow{AB}$=（-2，3），对角线交点为O，则$\overrightarrow{CO}$等于（-$\frac{1}{2}$，-5）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．己知a=${∫}_{0}^{\frac{π}{2}}$（$\frac{1}{2}$-sin2$\frac{x}{2}$）dx，则（ax+$\frac{1}{2ax}$）9展开式中，x的一次项系数为（　　）
    A．-$\frac{63}{16}$B．$\frac{63}{16}$C．-$\frac{63}{8}$D．$\frac{63}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在△ABC中，$\overrightarrow{MB}$=$\frac{1}{4}$$\overrightarrow{AB}$，且对AB边上任意一点N，恒有$\overrightarrow{NB}$•$\overrightarrow{NC}$≥$\overrightarrow{MB}$•$\overrightarrow{MC}$，则有（　　）
    A．AB⊥BCB．AB⊥ACC．AB=ACD．AC=BC

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=4sinx•sin2（$\frac{π}{4}$+$\frac{x}{2}$）+cos2x
    （1）设w＞0，且w为常数，若函数y=f（wx）在区间[-$\frac{π}{2}$，$\frac{2π}{3}$]上是增函数，求w的取值范围；
    （2）设集合A={x|$\frac{π}{6}$≤x≤$\frac{2π}{3}$}，B={x||f（x）-m|＜2}，若A∪B=B，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知向量$\overrightarrow a=（sin\frac{ωx}{2}，-sin\frac{ωx}{2}），\overrightarrow b=（cos\frac{ωx}{2}，sin\frac{ωx}{2}）（ω＞0）$，函数$f（x）=\overrightarrow a•\overrightarrow b$，x1，x2是函数f（x）的任意两个相异零点，且|x1-x2|的最小值为$\frac{π}{2}$．
    （Ⅰ）求ω的值；
    （Ⅱ）若函数g（x）=f（x）-m在$（0，\frac{π}{2}）$上无零点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．10名学生干部（名单见表2）进行内部评优，每人根据评分标准为自己和其他人打分，分值取0到10的整数．对某名干部的得分xi（i=1，2，…，10）计算均值$\overline x$和标准差s，计区间$（\overline x-2s，\overline x+2s）$内的得分我“有效得分”，则这名干部的最终得分为其有效得分的平均分，最终得分最高的前4名干部评为优秀干部．
    （1）表1为贝航的原始得分，请据此计算表2中a的值（保留两位小数），并判断贝航是否被评为了优秀干部；
    （2）现从这十名干部中随机抽取3人前往香港大学进行为期两天的交流访问，设所选取的3人中女生人数为X，优秀干部人数为Y，求概率P（X≥1且Y≥1）．
    表1
    姓名x1x2x3x4x5x6x7x8x9x10
    贝航99108996997
    表2
    姓名贝航黄韦嘉李萱刘紫璇罗迪威王安国肖悦杨清源袁佳仪周紫薇
    性别女男女女男男女男女女
    最终得分a9.228.508.818.438.918.127.959.317.79
    参考数据：$\sqrt{5}≈2.24$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若函数$f（x）=\frac{{{a^x}+1}}{{{a^x}-b}}（0＜a＜1）$的图象关于原点对称，则函数g（x）=loga（x+b）的大致图象是（　　）
    A．B．C．D．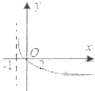

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知某几何体的三视图如图所示，其体积为$\frac{20}{3}$．

    查看答案和解析>>

    同步练习册答案