
| A. | AB⊥BC | B. | AB⊥AC | C. | AB=AC | D. | AC=BC |
分析 分别取AB,BC的中点D,E,将$\overrightarrow{NB}$•$\overrightarrow{NC}$表示为向量等式,得到$\overrightarrow{NB}$•$\overrightarrow{NC}$取最小值是的位置即可得到正确答案.
解答 解:分别取AB,BC的中点D,E,所以$\overrightarrow{NB}$•$\overrightarrow{NC}$=($\overrightarrow{EB}-\overrightarrow{EN}$)•($\overrightarrow{EC}-\overrightarrow{EN}$)=|NE|2-|BE|2,
当且仅当N到E的距离最小时,$\overrightarrow{NB}$•$\overrightarrow{NC}$取最小值,
由题意,N与M重合时$\overrightarrow{NB}$•$\overrightarrow{NC}$取得最小值,因此M到E的距离最近,
所以EM⊥AB,而CD∥EM,所以CD⊥AB,而CD是中线,
所以CA=CB;
故选D.
点评 本题考查了平面向量的运算;关键是结合几何图形得到不等式中等号成立时的位置.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:填空题
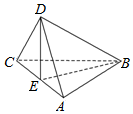 如图,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的有③(写出全部正确命题的序号).
如图,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的有③(写出全部正确命题的序号).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com