
分析 集合A={(x,y)|x2+y2=4}表示圆心为O,半径r为2的圆上所有点,且P在圆外,则有d(P,A)=|PO|-r,计算即可得到.对于D={P|d(P,A)≤1},讨论P在圆上和圆外及圆内,得到P的轨迹,运用圆的面积公式计算即可得到.
解答 解:集合A={(x,y)|x2+y2=4}表示圆心为O,半径r为2的圆上所有点,
点P的坐标为$(2\sqrt{2},2\sqrt{2})$,由|PO|=4>2,即有P在圆外,
那么d(P,A)=|PO|-r=4-2=2,
如果点集A所表示的图形是半径为2的圆,
若点P在圆上满足集合D,
P在圆外,则为介于圆心为O,半径分别为2,3的圆环,
其面积为9π-4π=5π,
P在圆内,则为介于圆心为O,半径分别为1,2的圆环,
其面积为4π-π=3π,
那么点集D={P|d(P,A)≤1}所表示的图形的面积为5π+3π=8π.
故答案为:2,8π.
点评 本题考查点和圆的位置关系,主要考查两点距离的最小值,理解点P到集合A的距离的新定义,并运用是解题的关键.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | AB⊥BC | B. | AB⊥AC | C. | AB=AC | D. | AC=BC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
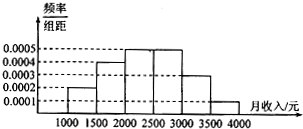 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图所示).为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2000,2500]月收入段应抽出( )
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图所示).为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2000,2500]月收入段应抽出( )| A. | 10人 | B. | 15人 | C. | 20人 | D. | 25人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com