
分析 (1)分a=0和a≠0两种情况讨论,对于后者利用跟的判别式求解即可;
(2)将不等式f(x)<g(x)转化为a<x+1+$\frac{2}{x}$,利用基本不等式解决即可
解答 解:(1)∵f(x)=ax2+x-2,
∴当a=0时,由f(x)=x-2=0得,函数f(x)有零点2,
当a≠0时,函数f(x)有零点等价于△=1-8a≥0,
即a$≤\frac{1}{8}$且a≠0,
综上可得,若函数f(x)有零点,求实数a的取值范围是(-∞,$\frac{1}{8}$];
(2)∵f(x)=ax2+x-2(a∈R),g(x)=x3+x2+3x-2,
∴不等式f(x)<g(x)可化为,
ax2<x3+x2+2x…①,
又∵x∈[1,3],
∴①可化为a$<x+1+\frac{2}{x}$,
根据基本不等式可知,x+1+$\frac{2}{x}$$≥2\sqrt{2}$+1,当且仅当x=$\sqrt{2}$时等号成立,
∴实数a的取值范围是(-∞,2$\sqrt{2}$+1).
点评 本题考查零点存在性定理,基本不等式的灵活应用,属于中档题


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“同位角相等,两直线平行”的逆否命题为:“两直线不平行,同位角不相等” | |
| B. | “若实数x,y满足x2+y2=0,则x,y全为0”的否命题为真命题 | |
| C. | 若p∧q为假命题,则p、q均为假命题 | |
| D. | 对于命题p:?x0∈R,${x_0}^2+2{x_0}+2≤0$,则?p:?x∈R,x2+2x+2>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
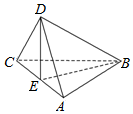 如图,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的有③(写出全部正确命题的序号).
如图,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的有③(写出全部正确命题的序号).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com