
若函数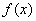 对任意的实数
对任意的实数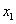 ,
,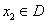 ,均有
,均有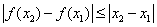 ,则称函数
,则称函数
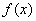 是区间
是区间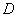 上的“平缓函数”
上的“平缓函数”
(1) 判断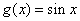 和
和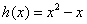 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由;
(2) 若数列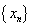 对所有的正整数
对所有的正整数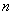 都有
都有 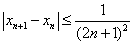 ,设
,设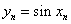 ,
,
求证:  .
.
(本小题主要考查函数、绝对值不等式等基础知识,考查函数与方程、分类与整合、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力、创新意识)
(1) 解: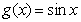 是R上的“平缓函数”,但
是R上的“平缓函数”,但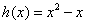 不是区间R的“平缓函数”;
不是区间R的“平缓函数”;
设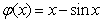 ,则
,则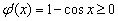 ,则
,则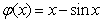 是实数集R上的增函数,
是实数集R上的增函数,
不妨设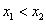 ,则
,则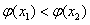 ,即
,即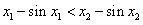 ,
,
则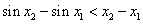 . ①
. ①
又 也是R上的增函数,则
也是R上的增函数,则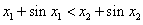 ,
,
即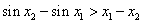 , ② …
, ② …
由①、②得 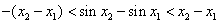 .
.
因此,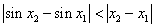 ,对
,对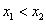 都成立.
都成立.
当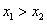 时,同理有
时,同理有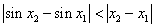 成立
成立
又当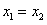 时,不等式
时,不等式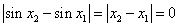 ,
,
故对任意的实数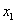 ,
,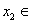 R,均有
R,均有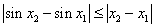 .
.
因此 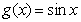 是R上的“平缓函数”.
是R上的“平缓函数”.
由于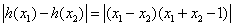
取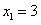 ,
,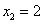 ,则
,则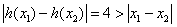 ,
,
因此, 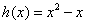 不是区间R的“平缓函数”.
不是区间R的“平缓函数”.
(2)证明:由(1)得: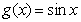 是R上的“平缓函数”,
是R上的“平缓函数”,
则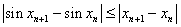 , 所以
, 所以 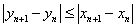 .
.
而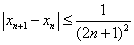 ,
,
∴ 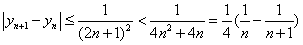 .
.
∵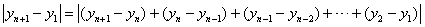 ,
,
∴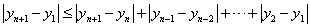 . …
. …
∴
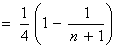
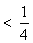 . ………
. ………


科目:高中数学 来源: 题型:
某人为了观看2008年奥运会,从2001年起每年5月10日到银行 存入a元定期储蓄,若年利率为p且保持不变,并且每年到期的存款及利息均自动转为新一年定期,到2008年将所有的存款和利息全部取回,则可取回的钱的总数(元)为( ).
存入a元定期储蓄,若年利率为p且保持不变,并且每年到期的存款及利息均自动转为新一年定期,到2008年将所有的存款和利息全部取回,则可取回的钱的总数(元)为( ).
A a(1+p)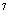 B a(1+p)
B a(1+p)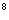 C
C 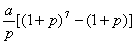 D
D 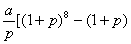 ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com