若两圆的半径分别为3和8.圆心距为13.试求两圆的外公切线的长度．题目和参考答案——青夏教育精英家教网—

16．若两圆的半径分别为3和8，圆心距为13，试求两圆的外公切线的长度．

分析本题考查两圆的位置关系．两圆的圆心距离大于两圆半径之和得出两圆相离关系，而后根据两圆外公切线定义来求长度．

解答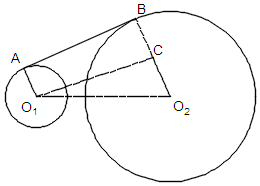解：由题意知两圆的半径R₁=3，R₂=8，且圆心距离O₁O₂=13；
∵O₁O₂＞R₁+R₂，∴圆O₁与圆O₂的位置关系为相离关系．
由右图可知AB为两圆的外公切线，O₁⊥AB，O₂⊥AB，
作O₁C∥AB 交线段BO₂于C点，故O₁C⊥BO₂，∴|AB|=$\sqrt{（{O}_{1}{O}_{2}）^{2}-（C{O}_{2}）^{2}}$
=$\sqrt{1{3}^{2}-（8-3）^{2}}$
=12，
故两圆的外公切线长度为12．

点评本题属于两圆的位置关系的常见考点，了解圆外公切线的定义．

练习册系列答案

智乐文化寒假作业期末综合复习东南大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

6．已知函数$f（x）=lnx+tanα（α∈（0，\frac{π}{2}））$的导函数为f′（x），若存在0＜x₀＜1使得f′（x₀）=f（x₀）成立，则实数α的取值范围是（$\frac{π}{4}$，$\frac{π}{2}$）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．与圆C₁：（x+3）²+y²=1，圆C₂：（x-3）²+y²=9同时外切的动圆圆心的轨迹方程是（　　）

A．

$\frac{y^2}{8}$-x²=1

B．

x²-$\frac{y^2}{8}$=1

C．

x²-$\frac{y^2}{8}$=1（x≥1）

D．

x²-$\frac{y^2}{8}$=1（x≤-1）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．

某城市理论预测2020年到2024年人口总数与年份的关系如表所示

年份x（年）	0	1	2	3	4
人口数y（十万）	5	7	8	11	19

（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
（3）据此估计2025年该城市人口总数．
参考公式：用最小二乘法求线性回归方程系数公式$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}，\hat a=\overline y-\hat b\overline x$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．（1）求值：sin²120°+cos180°+tan45°-cos²（-330°）+sin（-210°）；
（2）写出函数f（x）=${（{\frac{1}{3}}）^{sinx}}$的单调区间．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

1．已知函数f（x）=$\left\{\begin{array}{l}1+|lg（x-1）|，x＞1\\ g（x），x＜1\end{array}$的图象关于点P对称，且函数y=f（x+1）-1为奇函数，则下列结论：
①点P的坐标为（1，1）；
②当x∈（-∞，0）时，g（x）≤-1恒成立；
③关于x的方程f（x）=a，a∈R有且只有两个实根，
其中正确结论的个数为（　　）

A．

0个

B．

1个

C．

2个

D．

3个

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

8．若方程$\frac{x^2}{k-4}$+$\frac{y^2}{k+1}$=1表示的曲线是双曲线，则k的取值范围是（-1，4）．

查看答案和解析>>