
分析 由于f′(x)=$\frac{1}{x}$,f′(x0)=$\frac{1}{{x}_{0}}$,f′(x0)=f(x0),可得$\frac{1}{{x}_{0}}$=ln x0+tan α,即tan α=$\frac{1}{{x}_{0}}$-ln x0,由0<x0<1,可得$\frac{1}{{x}_{0}}$-ln x0>1,即tan α>1,即可得出.
解答 解:∵f′(x)=$\frac{1}{x}$,f′(x0)=$\frac{1}{{x}_{0}}$,f′(x0)=f(x0),
∴$\frac{1}{{x}_{0}}$=ln x0+tan α,
∴tan α=$\frac{1}{{x}_{0}}$-ln x0,
又∵0<x0<1,
∴可得$\frac{1}{{x}_{0}}$-ln x0>1,即tan α>1,
∴α∈($\frac{π}{4}$,$\frac{π}{2}$),
故答案为:($\frac{π}{4}$,$\frac{π}{2}$).
点评 本题考查了导数的运算法则、对数函数和正切函数的单调性,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>c>b | C. | a>b>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
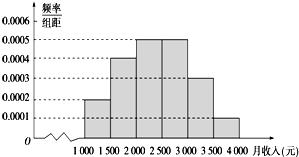 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com