
分析 (1)直接利用诱导公式以及特殊角化简求解即可.
(2)利用正弦函数的单调区间以及指数函数的单调性求解即可.
解答 解:(1)sin2120°+cos180°+tan45°-cos2(-330°)+sin(-210°)
=$\frac{3}{4}$-1+1-$\frac{3}{4}$+$\frac{1}{2}$
=$\frac{1}{2}$.
(2)函数f(x)=$(\frac{1}{3})^{x}$是减函数,y=sinx的增区间为:$[{\frac{π}{2}+2kπ,\frac{3π}{2}+2kπ}]$.k∈Z.
减区间为:$[{-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ}]$,k∈Z
所以函数f(x)=${({\frac{1}{3}})^{sinx}}$的增区间:$[{-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ}]$,减区间:$[{\frac{π}{2}+2kπ,\frac{3π}{2}+2kπ}]$.k∈Z.
点评 本题考查三角函数的化简求值,复合函数的单调性的求法,考查计算能力.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
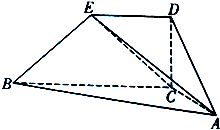 如图,AC=2,BC=4,∠ACB=$\frac{2}{3}$π,直角梯形BCDE中,BC∥DE,∠BCD=$\frac{π}{2}$,DE=2,且直线AE与CD所成角为$\frac{π}{3}$,AB⊥CD.
如图,AC=2,BC=4,∠ACB=$\frac{2}{3}$π,直角梯形BCDE中,BC∥DE,∠BCD=$\frac{π}{2}$,DE=2,且直线AE与CD所成角为$\frac{π}{3}$,AB⊥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com