
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� ��������$f��x��=\left\{\begin{array}{l}1-\left|x+1\right|��x��[-2��0]\\ 2f��x-2����x�ʣ�0��+�ޣ�\end{array}\right.$��ͼ�����ν�Ϸ��������������٣��ɵô𰸣�
��� �⣺����$f��x��=\left\{\begin{array}{l}1-\left|x+1\right|��x��[-2��0]\\ 2f��x-2����x�ʣ�0��+�ޣ�\end{array}\right.$��ͼ������ͼ��ʾ��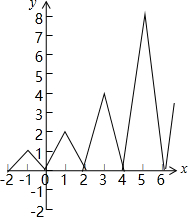
��ͼ�ɵã���f��x���ĵ����ݼ�����Ϊ[2n-3��2n-2]��n��N*�����ʢ���ȷ��
��f��x����ֵ��Ϊ[0��+�ޣ����ʢ���ȷ��
����-2��a��0����f��x��=x+a������[-2��0]����������2������ȵ�ʵ�����ʢ۴���
��ѡ��C
���� ���������������ж���Ӧ��Ϊ���壬�����˺�����ͼ������ֵ�����ĸ��뷽�̵���㣬�Ѷ��е���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 3 | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
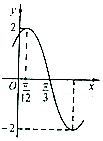 ��֪����f��x��=Asin����x+ϕ����A��0���أ�0��f��x��=Asin����x+�գ��IJ���ͼ����ͼ��ʾ������˵����ȷ���ǣ�������
��֪����f��x��=Asin����x+ϕ����A��0���أ�0��f��x��=Asin����x+�գ��IJ���ͼ����ͼ��ʾ������˵����ȷ���ǣ�������| A�� | ����f��x������С������Ϊ2�� | |
| B�� | ����f��x����ͼ����ڵ�$��{-\frac{5��}{12}��0}��$�Գ� | |
| C�� | ������f��x����ͼ������ƽ��$\frac{��}{6}$����λ�õ��ĺ���ͼ�����y��Գ� | |
| D�� | ����f��x���ĵ�������������$[{k��+\frac{7��}{12}��k��+\frac{13��}{12}}]��k��Z$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{{\sqrt{2}}}{4}$ | B�� | $-\frac{{\sqrt{2}}}{2}$ | C�� | $\frac{{\sqrt{2}}}{4}$ | D�� | $\frac{{\sqrt{2}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֶ��DZ�Ҫ���� | B�� | ��Ҫ���dz������ | ||
| C�� | ��Ҫ���� | D�� | �ȷdz��Ҳ�DZ�Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | e+1 | B�� | e+$\frac{1}{2}$ | C�� | $\frac{e}{2}$ | D�� | $\frac{e}{4}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com