
| A. | e+1 | B. | e+$\frac{1}{2}$ | C. | $\frac{e}{2}$ | D. | $\frac{e}{4}$ |
分析 利用不等式ex-(a+1)x-b≥0(e为自然对数的底数)在R上恒成立,利用导函数研究单调性求出a,b的关系,再次利用导函数研究单调性(a+1)b的最大值.
解答 解:不等式ex-(a+1)x-b≥0(e为自然对数的底数)在R上恒成立,令f(x)=ex-(a+1)x-b,则f(x)≥0在R上恒成立.
只需要f(x)min≥0即可.
f′(x)=ex-(a+1)
令f′(x)=0,
解得x=ln(a+1),(a>-1)
当x∈(-∞,ln(a+1))时,f′(x)<0,则f(x)时单调递减.
当x∈(ln(a+1),+∞)时,f′(x)>0,则f(x)时单调递增.
故x=ln(a+1)时,f(x)取得最小值
即(a+1)-(a+1)ln(a+1)≥b
那么:(a+1)2[1-ln(a+1)]≥b(a+1)
令(a+1)=t,(t>0)
则现求g(t)=t2-t2lnt的最大值.
g′(t)=$2t-2t•lnt-\frac{1}{t}•{t}^{2}$
令g′(t)=0,解得:t=${e}^{\frac{1}{2}}$
得极大值为g(${e}^{\frac{1}{2}}$)=$\frac{e}{2}$
∴(a+1)b的最大值为$\frac{e}{2}$.
故选C.
点评 本题考查导数与函数的单调性、极值、最值与函数与方程,属难题;


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | af(b)≤bf(a) | B. | bf(a)≤af(b) | C. | af(a)≤bf(b) | D. | bf(b)≤af(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
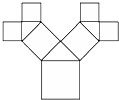 如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )
如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )| A. | $\frac{1}{64}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<4} | B. | {x|-1<x≤4} | C. | {x|4≤x<10} | D. | {x|-1≤x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {(0,1),(1,0)} | C. | {(0,1)} | D. | {(1,0)} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com