
分析 由题意:x∈[0,1),x与a满足关系式(2-a)ea=x(2+a),求解a的值,化简f(x)可得其值域.
解答 解:由题意:x∈[0,1),x与a满足关系式(2-a)ea=x(2+a),
则x=$\frac{(2-a){e}^{a}}{2+a}$,
①当x=0时,可得:(2-a)•ea=0,
解得:a=2.
那么:函数f(x)=$\frac{{{a^2}{e^a}}}{{{e^a}-(a+1)x}}$=$\frac{4{e}^{2}}{{e}^{2}-3x}$=a2=4.
②当x≠0时,可得:${e}^{a}=\frac{x(2+a)}{2-a}$,此时函数f(x)=$\frac{{a}^{2}}{1-\frac{(a+1)x}{{e}^{a}}}$=$\frac{{a}^{2}}{1-(a+1)x•\frac{2-a}{x(2+a)}}=a+2$
令a+2=t,则(4-t)et-2=x•t,且a≠0,可得t≠2.
得:x=$\frac{4-t}{t}•{e}^{t-2}$,
∵x∈(0,1),et-2>0,
∴$\frac{4-t}{t}>0$,
解得:0<t<4,
令f(t)=$\frac{4-t}{t}•{e}^{t-2}$,
则f′(t)=-$\frac{{e}^{t}(t-2)^{2}}{(et)^{2}}$在t∈(0,4)恒小于0.
∴f(t)在t∈(0,4)上单调递减
由于x=f(t)∈(0,1),
当t=2时,f(t)=1,当t=4时,f(t)=0,
则2<t<4,即此时f(x)的值域为(2,4).
综上可得:函数f(x)=$\frac{{{a^2}{e^a}}}{{{e^a}-(a+1)x}}$的值域是(2,4].
故答案为(2,4].
点评 本题考查了导函数研究值域的方法,利用其单调性和转化思想,分类讨论,构造新的函数求其值域来达到解决原函数的值域问题.属于难题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而非必要条件 | B. | 必要而非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
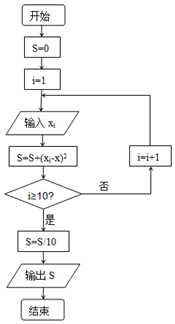 三月植树节,林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
三月植树节,林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{5π}{6}$) | B. | (2,$\frac{2π}{3}$) | C. | (2,$\frac{5π}{3}$) | D. | (2,$\frac{11π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e+1 | B. | e+$\frac{1}{2}$ | C. | $\frac{e}{2}$ | D. | $\frac{e}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$-1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com