
分析 把不等式化为$\frac{1}{{(x-1)}^{2}}$>$\frac{1}{{(2+x)}^{2}}$,解分式不等式即可.
解答 解:不等式(x-1)-2>(2+x)-2可化为$\frac{1}{{(x-1)}^{2}}$>$\frac{1}{{(2+x)}^{2}}$,
即(2+x)2>(x-1)2>0,
解得$\left\{\begin{array}{l}{x-1≠0}\\{(2+x+x-1)(2+x-x+1)>0}\end{array}\right.$,
即x>-$\frac{1}{2}$,且x≠1;
∴x的取值范围是{x|x>-$\frac{1}{2}$,且x≠1}.
故答案为:{x|x>-$\frac{1}{2}$,且x≠1}.
点评 本题考查了不等式的解法与应用问题,也考查了转化思想的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
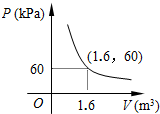 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$m3 | B. | 小于$\frac{5}{4}$m3 | C. | 不小于$\frac{4}{5}$m3 | D. | 不大于$\frac{4}{5}$m3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | (3,+∞) | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com