练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线l和平面，若直线l在空间中任意放置，则在平面内总有直线和

    A.垂直B.平行C.异面D.相交

    【答案】A

    【解析】

    本题可以从直线与平面的位置关系入手：直线与平面的位置关系可以分为三种：直线在平面内、直线与平面相交、直线与平面平行，在这三种情况下再讨论平面中的直线与已知直线的关系，通过比较可知：每种情况都有可能垂直．

    当直线l与平面相交时，

    平面内的任意一条直线与直线l的关系只有两种：异面、相交，此时就不可能平行了，故B错．

    当直线l与平面平行时，

    平面内的任意一条直线与直线l的关系只有两种：异面、平行，此时就不可能相交了，故D错．

    当直线a在平面内时，

    平面内的任意一条直线与直线l的关系只有两种：平行、相交，此时就不可能异面了，故C错．

    不管直线l与平面的位置关系相交、平行，还是在平面内，

    都可以在平面内找到一条直线与直线垂直，

    因为直线在异面与相交时都包括垂直的情况，故A正确．

    故选:A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设圆的圆心为A，直线l过点B（1,0）且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

    （I）证明为定值，并写出点E的轨迹方程；

    （II）设点E的轨迹为曲线C1，直线l交C1于M,N两点，过B且与l垂直的直线与圆A交于P,Q两点，求四边形MPNQ面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知{an}是等差数列，其中a1=25，a4=16

    （1）数列{an}从哪一项开始小于0；

    （2）求a1+a3+a5+…+a19值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB为圆O的直径，点E、F在圆O上，ABEF，矩形ABCD所在平面和圆O所在平面垂直，已知AB＝2，EF＝1．

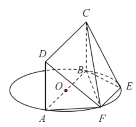
    （I）求证：平面DAF⊥平面CBF；

    （II）若BC＝1，求四棱锥F－ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是方程的两根，数列是递增的等差数列，数列的前项和为，且.

    （1）求数列的通项公式；

    （2）记，求数列的前和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，，，和均为边长为的等边三角形.

    （1）求证：平面平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,矩形和菱形所在的平面相互垂直,,为的中点.

    (1)求证：平面；

    (2)若,求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知以M点为圆心的圆及其上一点.

    （1）设圆N与y轴相切，与圆M外切，且圆心在直线上，求圆N的标准方程；

    （2）设平行于OA的直线l与圆M相交于B，C两点且，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出，将冰雪这个冷项目迅速炒“热”．北京某综合大学计划在一年级开设冰球课程，为了解学生对冰球运动的兴趣，随机从该校一年级学生中抽取了100人进行调查，其中女生中对冰球运动有兴趣的占，而男生有10人表示对冰球运动没有兴趣额．

    （1）完成列联表，并回答能否有的把握认为“对冰球是否有兴趣与性别有关”？

    （2）若将频率视为概率，现再从该校一年级全体学生中，采用随机抽样的方法每次抽取1名学生，抽取5次，记被抽取的5名学生中对冰球有兴趣的人数为，若每次抽取的结果是相互独立的，求的分布列，期望和方差．

    附表：

    查看答案和解析>>

    同步练习册答案