
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() 均为边长为
均为边长为![]() 的等边三角形.
的等边三角形.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1) 取![]() 的中点
的中点![]() ,连接
,连接![]() ,要证平面
,要证平面![]() 平面
平面![]() ,转证
,转证![]() 平面
平面![]() ,即证
,即证![]() ,
,![]() 即可;(2) 以
即可;(2) 以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴正方向,建立如图所示的空间直角坐标系,分别求出平面
轴正方向,建立如图所示的空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的法向量,代入公式,即可得到结果.
的法向量,代入公式,即可得到结果.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() 均为边长为
均为边长为![]() 的等边三角形,
的等边三角形,
所以![]() ,
,![]() ,且
,且![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)因为![]() ,
,![]() 为等边三角形,
为等边三角形,
所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,![]() ,
,
在![]() 中,由正弦定理,得:
中,由正弦定理,得:![]() ,所以
,所以![]() .
.
以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴正方向,建立如图所示的空间直角坐标系,
轴正方向,建立如图所示的空间直角坐标系,
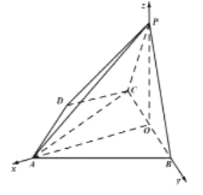
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则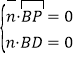 ,即
,即![]() ,
,
令![]() ,则平面
,则平面![]() 的一个法向量为
的一个法向量为![]() ,
,
依题意,平面![]() 的一个法向量
的一个法向量![]()
所以![]()
故二面角![]() 的余弦值为
的余弦值为![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】若从装有![]() 个红球和
个红球和![]() 个黑球的口袋内任取
个黑球的口袋内任取![]() 个球,则下列为互斥的两个事件是( )
个球,则下列为互斥的两个事件是( )
A.“至少有一个黑球”与“都是黑球”B.“一个红球也没有”与“都是黑球”
C.“至少有一个红球”与“都是红球”D.“恰有![]() 个黑球”与“恰有
个黑球”与“恰有![]() 个黑球”
个黑球”
查看答案和解析>>
科目:高中数学 来源: 题型:
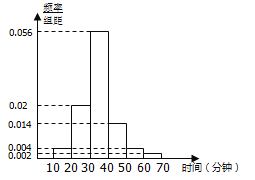
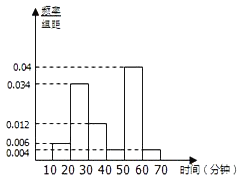
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.
![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届世界低碳经济大会近日召开,本届大会的主题为“节能减排,绿色生态”.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为![]() 吨,最多为
吨,最多为![]() 吨,月处理成本
吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为
,且每处理一吨二氧化碳得到可利用的化工产品价值为![]() 元.
元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》第七章“盈不足”中有一道两鼠穿墙问题:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何”,翻译过来就是:有五尺厚的墙,两只老鼠从墙的两边相对分别打洞穿墙,大、小鼠第一天都进一尺,以后每天,大鼠加倍,小鼠减半,则几天后两鼠相遇,这个问题体现了古代对数列问题的研究,现将墙的厚度改为1200尺,则需要几天时间才能打穿(结果取整数)( )
A.12B.11C.10D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②请根据相关信息,解答下列问题:


(1)图①中![]() 的值为___________;
的值为___________;
(2)统计这组数据的平均数众数和中位数;
(3)根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定:在桌面上,用母球击打目标球,使目标球运动,球的位置是指球心的位置,我们说球 A 是指该球的球心点 A.两球碰撞后,目标球在两球的球心所确定的直线上运动,目标球的运动方向是指目标球被母球击打时,母球球心所指向目标球球心的方向.所有的球都简化为平面上半径为 1 的圆,且母球与目标球有公共点时,目标球就开始运动,在桌面上建立平面直角坐标系,解决下列问题:

(1) 如图,设母球 A 的位置为 (0, 0),目标球 B 的位置为 (4, 0),要使目标球 B 向 C(8, -4) 处运动,求母球 A 球心运动的直线方程;
(2)如图,若母球 A 的位置为 (0, -2),目标球 B 的位置为 (4, 0),能否让母球 A 击打目标 B 球后,使目标 B 球向 (8,-4) 处运动?
(3)若 A 的位置为 (0,a) 时,使得母球 A 击打目标球 B 时,目标球 B(4![]() , 0) 运动方向可以碰到目标球 C(7
, 0) 运动方向可以碰到目标球 C(7![]() ,-5
,-5![]() ),求 a 的最小值(只需要写出结果即可)
),求 a 的最小值(只需要写出结果即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com