
分析 由x2-2>x,解得x>2,或x<-1.可得f(x)=$\left\{\begin{array}{l}{{x}^{2}+x-2,x>2或x<-1}\\{{x}^{2}-x-2,-1≤x≤2}\end{array}\right.$,通过分类讨论,利用二次函数的单调性即可得出.
解答 解:由x2-2>x,解得x>2,或x<-1.
∴f(x)=$\left\{\begin{array}{l}{{x}^{2}+x-2,x>2或x<-1}\\{{x}^{2}-x-2,-1≤x≤2}\end{array}\right.$,
①-1≤x≤2时,f(x)=x2-x-2=$(x-\frac{1}{2})^{2}$-$\frac{9}{4}$,可知:函数f(x)在$[-1,\frac{1}{2}]$内单调递减;在$(\frac{1}{2},2]$内单调递增.
f(-1)=0,f(2)=0.∴f(x)∈$[-\frac{9}{4},0]$.
②x>2,或x<-1时,f(x)=x2+x-2=$(x+\frac{1}{2})^{2}$-$\frac{9}{4}$,利用单调性可得:f(x)>f(-1)=-2,或f(x)>f(2)=4,可得f(x)∈(-2,+∞).
综上可得:f(x)∈$[-\frac{9}{4},+∞)$.
故答案为:$[-\frac{9}{4},+∞)$.
点评 本题考查了分段函数的应用、不等式的解法、二次函数的单调性,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (2,+∞) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?c>0,方程x2-x+c=0无解 | B. | ?c≤0,方程x2-x+c=0有解 | ||
| C. | ?c>0,方程x2-x+c=0无解 | D. | ?c<0,方程x2-x+c=0有解 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{7}{9}$ | B. | $±\frac{{4\sqrt{2}}}{7}$ | C. | $±2\sqrt{2}$ | D. | $±\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
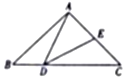 如图所示,在△ABC中,点D为BC边上一点,且BD=1,E为AC的中点,AE=$\frac{3}{2}$,cosB=$\frac{{2\sqrt{7}}}{7}$,∠ADB=$\frac{2π}{3}$.
如图所示,在△ABC中,点D为BC边上一点,且BD=1,E为AC的中点,AE=$\frac{3}{2}$,cosB=$\frac{{2\sqrt{7}}}{7}$,∠ADB=$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 4π | C. | 5π | D. | 8π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com