
【题目】华为董事会决定投资开发新款软件,估计能获得![]() 万元到
万元到![]() 万元的投资收益,讨论了一个对课题组的奖励方案:奖金
万元的投资收益,讨论了一个对课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .
.
(1)请分析函数![]() 是否符合华为要求的奖励函数模型,并说明原因;
是否符合华为要求的奖励函数模型,并说明原因;
(2)若华为公司采用模型函数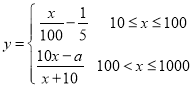 作为奖励函数模型,试确定正整数
作为奖励函数模型,试确定正整数![]() 的取值集合.
的取值集合.
【答案】(1)不符合,原因见解析(2)![]() 的取值集合为
的取值集合为![]()
【解析】
(1)根据题意,总结奖励模型需要满足的条件①![]() 在定义域
在定义域![]() 上是增函数;②
上是增函数;②![]() 恒成立;③
恒成立;③![]() 恒成立;判断单调性及最值,即可求解;
恒成立;判断单调性及最值,即可求解;
(2)由题意,依此判断分段函数的单调性,最大值和![]() ,即可求解参数范围,由
,即可求解参数范围,由![]() 为正整数,即可确定取值集合.
为正整数,即可确定取值集合.
(1)设奖励函数模型为![]() ,按公司对函数模型的基本要求,函数
,按公司对函数模型的基本要求,函数![]() 满足:当
满足:当![]() 时,①
时,①![]() 在定义域
在定义域![]() 上是增函数;②
上是增函数;②![]() 恒成立;③
恒成立;③![]() 恒成立.对于函数模型
恒成立.对于函数模型![]() .当
.当![]() 时,
时,![]() 是增函数,
是增函数,![]() 所以
所以![]() 不恒成立.故该函数模型不符合公司要求.
不恒成立.故该函数模型不符合公司要求.
(2)对于函数模型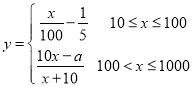 ,当
,当![]() 时,
时,![]() 在定义域
在定义域![]() 上是增函数,且
上是增函数,且![]() 恒成立;当
恒成立;当![]() 时,
时,![]() ,只有
,只有 时,
时,![]() 在定义域
在定义域![]() 上是增函数;要使
上是增函数;要使![]() 在
在![]() 恒成立,
恒成立,![]() ,即
,即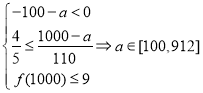 ;要使
;要使![]() 恒成立对
恒成立对![]() 恒成立,即
恒成立,即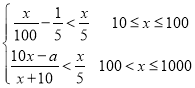 ,即
,即![]() 恒成立,所以
恒成立,所以![]() ;
;
综上所述,![]() ,所以满足条件的正整数a的取值集合为
,所以满足条件的正整数a的取值集合为![]()


科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为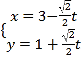 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为(3,1),求
的坐标为(3,1),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(Ⅰ)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(Ⅱ)设椭圆C的右焦点为F,点Q在y轴上,且∠PFQ=90°,求证:AQ∥BM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用希腊字母![]() 表示.早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第7位的人,这比欧洲早了约1000年.生活中,我们也可以通过如下随机模拟试验来估计
表示.早在公元480年左右,南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果,他是世界上第一个把圆周率的数值计算到小数点后第7位的人,这比欧洲早了约1000年.生活中,我们也可以通过如下随机模拟试验来估计![]() 的值:在区间
的值:在区间![]() 内随机取
内随机取![]() 个数,构成
个数,构成![]() 个数对
个数对![]() ,设
,设![]() ,
,![]() 能与1构成钝角三角形三边的数对
能与1构成钝角三角形三边的数对![]() 有
有![]() 对,则通过随机模拟的方法得到的
对,则通过随机模拟的方法得到的![]() 的近似值为( )
的近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到直线
到直线![]() 的距离比到定点
的距离比到定点![]() 的距离大1.
的距离大1.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)若![]() 为直线
为直线![]() 上一动点,过点
上一动点,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
①求证:![]() 轴;
轴;
②直线![]() 是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市抽查了100天该超市的日纯利润数据,并将日纯利润数据分成以下几组(单位:万元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计结果如下表所示:
,统计结果如下表所示:
组别 |
|
|
|
|
|
|
频数 | 5 | 20 | 30 | 30 | 10 | 5 |
以上述样本分布的频率估计总体分布的概率,解决下列问题:
(1)从该大型超市近几年的销售记录中抽出5天,求其中日纯利润在区间![]() 内的天数不少于2的概率;
内的天数不少于2的概率;
(2)该超市经理由频数分布表可以认为,该大型超市每天的纯利润![]() 服从正态分布
服从正态分布![]() ,其中,
,其中,![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值).
(每组数据取区间的中点值).
①试利用该正态分布,估计该大型超市1000天内日纯利润在区间![]() 内的天数(精确到个位);
内的天数(精确到个位);
②该大型超市负责人根据每日的纯利润给超市员工制定了两种不同的奖励方案:
方案一:直接发放奖金,日纯利润低于![]() 时每名员工发放奖金70元,日纯利润不低于
时每名员工发放奖金70元,日纯利润不低于![]() 时每名员工发放奖金90元;
时每名员工发放奖金90元;
方案二:利用抽奖的方式获得奖金,其中日纯利润不低于![]() 时每位员工均有两次抽奖机会,日纯利润低于
时每位员工均有两次抽奖机会,日纯利润低于![]() 时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
金额 | 50元 | 100元 |
概率 |
|
|
小张恰好为该大型超市的一名员工,则从数学期望的角度看,小张选择哪种奖励方案更有利?
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com