
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() .
.
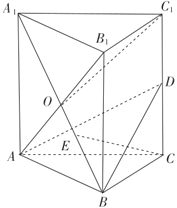
(1)证明:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的正切值为
的正切值为![]() ,
,![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,直线
,直线![]() 过椭圆的
过椭圆的![]() 左焦点.
左焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 的平分线在
的平分线在![]() 轴上,
轴上,![]() .试判断直线
.试判断直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为董事会决定投资开发新款软件,估计能获得![]() 万元到
万元到![]() 万元的投资收益,讨论了一个对课题组的奖励方案:奖金
万元的投资收益,讨论了一个对课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .
.
(1)请分析函数![]() 是否符合华为要求的奖励函数模型,并说明原因;
是否符合华为要求的奖励函数模型,并说明原因;
(2)若华为公司采用模型函数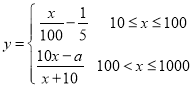 作为奖励函数模型,试确定正整数
作为奖励函数模型,试确定正整数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为了调查该校学生性别与身高的关系,对该校1000名学生按照![]() 的比例进行抽样调查,得到身高频数分布表如下:
的比例进行抽样调查,得到身高频数分布表如下:
男生身高频率分布表
男生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 7 | 10 | 19 | 18 | 4 | 2 |
女生身高频数分布表
女生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 3 | 10 | 15 | 6 | 3 | 3 |
(1)估计这1000名学生中女生的人数;
(2)估计这1000名学生中身高在![]() 的概率;
的概率;
(3)在样本中,从身高在![]() 的女生中任取3名女生进行调查,设
的女生中任取3名女生进行调查,设![]() 表示所选3名学生中身高在
表示所选3名学生中身高在![]() 的人数,求
的人数,求![]() 的分布列和数学期望.(身高单位:厘米)
的分布列和数学期望.(身高单位:厘米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点的椭圆E的一个焦点与抛物线![]() 的焦点关于直线
的焦点关于直线![]() 对称,且椭圆E与坐标轴的一个交点坐标为
对称,且椭圆E与坐标轴的一个交点坐标为![]() .
.
(1)求椭圆E的标准方程;
(2)过点![]() 的直线l(直线的斜率k存在且不为0)交E于A,B两点,交x轴于点P点A关于x轴的对称点为D,直线BD交x轴于点Q.试探究
的直线l(直线的斜率k存在且不为0)交E于A,B两点,交x轴于点P点A关于x轴的对称点为D,直线BD交x轴于点Q.试探究![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,其右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
![]() 求椭圆C的方程;
求椭圆C的方程;
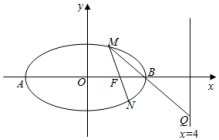
![]() 设椭圆的左、右顶点分别为A、B,M是椭圆上异于A,B的任意一点,直线MF交椭圆C于另一点N,直线MB交直线
设椭圆的左、右顶点分别为A、B,M是椭圆上异于A,B的任意一点,直线MF交椭圆C于另一点N,直线MB交直线![]() 于Q点,求证:A,N,Q三点在同一条直线上.
于Q点,求证:A,N,Q三点在同一条直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一名高二学生盼望2020年进入某名牌大学学习,假设该名牌大学有以下条件之一均可录取:①2020年2月通过考试进入国家数学奥赛集训队(集训队从2019年10月省数学竞赛一等奖中选拔):②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线,③2020年6月高考达到该校录取分数线(该校录取分数线高于重点线),该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖,则该学生估计进入国家集训队的概率是0.2.若进入国家集训队,则提前录取,若未被录取,则再按②、③顺序依次录取:前面已经被录取后,不得参加后面的考试或录取.(注:自主招生考试通过且高考达重点线才能录取)
(Ⅰ)求该学生参加自主招生考试的概率;
(Ⅱ)求该学生参加考试的次数![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)求该学生被该校录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解市民对开设传统文化课的态度,教育机构随机抽取了![]() 位市民进行了解,发现支持开展的占
位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民
,在抽取的男性市民![]() 人中持支持态度的为
人中持支持态度的为![]() 人.
人.
(1)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?
支持 | 不支持 | 合计 | |
男性 | |||
女性 | |||
合计 |
(2)为了进一步征求对开展传统文化的意见和建议,从抽取的![]() 位市民中对不支持的按照分层抽样的方法抽取
位市民中对不支持的按照分层抽样的方法抽取![]() 位市民,并从抽取的
位市民,并从抽取的![]() 人中再随机选取
人中再随机选取![]() 人进行座谈,求选取的
人进行座谈,求选取的![]() 人恰好为
人恰好为![]() 男
男![]() 女的概率.
女的概率.
附: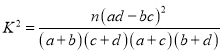
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com