
ЁОЬтФПЁПдкШЋУцПЙЛїаТЙкЗЮбзвпЧщетвЛЬиЪтЪБЦкЃЌЮвЪаНЬг§ОжЬсГіЁАЭЃПЮВЛЭЃбЇЁБЕФПкКХЃЌЙФРјбЇЩњЯпЩЯбЇЯА.ФГаЃЪ§бЇНЬЪІЮЊСЫЕїВщИпШ§бЇЩњЪ§бЇГЩМЈгыЯпЩЯбЇЯАЪБМфжЎМфЕФЯрЙиЙиЯЕЃЌЖдИпШ§ФъМЖЫцЛњбЁШЁ45УћбЇЩњНјааИњзйЮЪОэЃЌЦфжаУПжмЯпЩЯбЇЯАЪ§бЇЪБМфВЛЩйгк5аЁЪБЕФга19ШЫЃЌгрЯТЕФШЫжаЃЌдкМьВтПМЪджаЪ§бЇЦНОљГЩМЈВЛзу120ЗжЕФеМ![]() ЃЌЭГМЦГЩМЈКѓЕУЕНШчЯТ
ЃЌЭГМЦГЩМЈКѓЕУЕНШчЯТ![]() СаСЊБэЃК
СаСЊБэЃК
ЗжЪ§ВЛЩйгк120Зж | ЗжЪ§ВЛзу120Зж | КЯМЦ | |
ЯпЩЯбЇЯАЪБМфВЛЩйгк5аЁЪБ | 4 | 19 | |
ЯпЩЯбЇЯАЪБМфВЛзу5аЁЪБ | |||
КЯМЦ | 45 |
ЃЈ1ЃЉЧыЭъГЩЩЯУц![]() СаСЊБэЃЛВЂХаЖЯЪЧЗёга99%ЕФАбЮеШЯЮЊЁАИпШ§бЇЩњЕФЪ§бЇГЩМЈгыбЇЩњЯпЩЯбЇЯАЪБМфгаЙиЁБЃЛ
СаСЊБэЃЛВЂХаЖЯЪЧЗёга99%ЕФАбЮеШЯЮЊЁАИпШ§бЇЩњЕФЪ§бЇГЩМЈгыбЇЩњЯпЩЯбЇЯАЪБМфгаЙиЁБЃЛ
ЃЈ2ЃЉЂйАДееЗжВуГщбљЕФЗНЗЈЃЌдкЩЯЪібљБОжаДгЗжЪ§ВЛЩйгк120ЗжКЭЗжЪ§ВЛзу120ЗжЕФСНзщбЇЩњжаГщШЁ9УћбЇЩњЃЌЩшГщЕНВЛзу120ЗжЧвУПжмЯпЩЯбЇЯАЪБМфВЛзу5аЁЪБЕФШЫЪ§ЪЧ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаЃЈИХТЪгУзщКЯЪ§ЫуЪНБэЪОЃЉЃЛ
ЕФЗжВМСаЃЈИХТЪгУзщКЯЪ§ЫуЪНБэЪОЃЉЃЛ
ЂкШєНЋЦЕТЪЪгЮЊИХТЪЃЌДгШЋаЃИпШ§ИУДЮМьВтЪ§бЇГЩМЈВЛЩйгк120ЗжЕФбЇЩњжаЫцЛњГщШЁ20ШЫЃЌЧѓетаЉШЫжаУПжмЯпЩЯбЇЯАЪБМфВЛЩйгк5аЁЪБЕФШЫЪ§ЕФЦкЭћКЭЗНВю.
ЃЈЯТУцЕФСйНчжЕБэЙЉВЮПМЃЉ
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ЃЈВЮПМЙЋЪН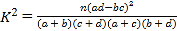 Цфжа
Цфжа![]() ЃЉ
ЃЉ
ЁОД№АИЁПЃЈ1ЃЉЬюБэМћНтЮіЃЛга99%ЕФАбЮеШЯЮЊЁАИпШ§бЇЩњЕФЪ§бЇГЩМЈгыбЇЩњЯпЩЯбЇЯАЪБМфгаЙиЁБЃЈ2ЃЉЂйЯъМћНтЮіЂкЦкЭћ![]() ЃЛЗНВю
ЃЛЗНВю![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЭъГЩСаСЊБэЃЌДњШыЪ§ОнМДПЩХаЖЯЃЛ
ЃЈ2ЃЉРћгУЗжВуГщбљПЩЕУ![]() ЕФШЁжЕЃЌНјЖјЕУЕНИХТЪЃЌСаГіЗжВМСаЃЛИљОнЗжЮіжЊ
ЕФШЁжЕЃЌНјЖјЕУЕНИХТЪЃЌСаГіЗжВМСаЃЛИљОнЗжЮіжЊ![]() ЃЌМЦЫуГіЦкЭћгыЗНВю.
ЃЌМЦЫуГіЦкЭћгыЗНВю.
ЃЈ1ЃЉ
ЗжЪ§ВЛЩйгк120Зж | ЗжЪ§ВЛзу120Зж | КЯМЦ | |
ЯпЩЯбЇЯАЪБМфВЛЩйгк5аЁЪБ | 15 | 4 | 19 |
ЯпЩЯбЇЯАЪБМфВЛзу5аЁЪБ | 10 | 16 | 26 |
КЯМЦ | 25 | 20 | 45 |
![]()
![]() га99%ЕФАбЮеШЯЮЊЁАИпШ§бЇЩњЕФЪ§бЇГЩМЈгыбЇЩњЯпЩЯбЇЯАЪБМфгаЙиЁБ.
га99%ЕФАбЮеШЯЮЊЁАИпШ§бЇЩњЕФЪ§бЇГЩМЈгыбЇЩњЯпЩЯбЇЯАЪБМфгаЙиЁБ.
ЃЈ2ЃЉЂйгЩЗжВуГщбљжЊЃЌашвЊДгВЛзу120ЗжЕФбЇЩњжаГщШЁ![]() ШЫЃЌ
ШЫЃЌ
![]() ЕФПЩФмШЁжЕЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4ЃЌ
ЕФПЩФмШЁжЕЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЫљвдЃЌ![]() ЕФЗжВМСаЃК
ЕФЗжВМСаЃК
|
|
|
|
|
|
|
|
|
|
|
|
ЂкДгШЋаЃВЛЩйгк120ЗжЕФбЇЩњжаЫцЛњГщШЁ1ШЫЃЌДЫШЫУПжмЩЯЯпЪБМфВЛЩйгк5аЁЪБЕФИХТЪЮЊ![]() ЃЌЩшДгШЋаЃВЛЩйгк120ЗжЕФбЇЩњжаЫцЛњГщШЁ20ШЫЃЌетаЉШЫжаУПжмЯпЩЯбЇЯАЪБМфВЛЩйгк5аЁЪБЕФШЫЪ§ЮЊ
ЃЌЩшДгШЋаЃВЛЩйгк120ЗжЕФбЇЩњжаЫцЛњГщШЁ20ШЫЃЌетаЉШЫжаУПжмЯпЩЯбЇЯАЪБМфВЛЩйгк5аЁЪБЕФШЫЪ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЙЪ![]() ЃЌ
ЃЌ![]() .
.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВ![]() ЕФдВаФЮЊ
ЕФдВаФЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧдВ
ЪЧдВ![]() ФквЛИіЖЈЕуЃЌЕу
ФквЛИіЖЈЕуЃЌЕу![]() ЪЧдВ
ЪЧдВ![]() ЩЯШЮвтвЛЕуЃЌЯпЖЮ
ЩЯШЮвтвЛЕуЃЌЯпЖЮ![]() ЕФДЙжБЦНЗжЯпгыАыОЖ
ЕФДЙжБЦНЗжЯпгыАыОЖ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() .
.
ЃЈ1ЃЉЧѓЖЏЕу![]() ЕФЙьМЃ
ЕФЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉИјЖЈЕу![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() ВЛОЙ§Еу
ВЛОЙ§Еу![]() ЧвгыЙьМЃ
ЧвгыЙьМЃ![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌвдЯпЖЮ
СНЕуЃЌвдЯпЖЮ![]() ЮЊжБОЖЕФдВЙ§Еу
ЮЊжБОЖЕФдВЙ§Еу![]() .жЄУїЃКжБЯп
.жЄУїЃКжБЯп![]() Й§ЖЈЕу.
Й§ЖЈЕу.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉЮЊЦцКЏЪ§ЃЌЧвЕБxЁн0ЪБЃЌfЃЈxЃЉЃНexЉcosxЃЌдђВЛЕШЪНfЃЈ2xЉ1ЃЉ+fЃЈxЉ2ЃЉЃО0ЕФНтМЏЮЊ( )
A.ЃЈЉЁоЃЌ1ЃЉB.ЃЈЉЁоЃЌ![]() ЃЉC.ЃЈ
ЃЉC.ЃЈ![]() ЃЌ+ЁоЃЉD.ЃЈ1ЃЌ+ЁоЃЉ
ЃЌ+ЁоЃЉD.ЃЈ1ЃЌ+ЁоЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЃЈ
ЃЈ![]() ЃЉЕФгвЖЅЕуЮЊ
ЃЉЕФгвЖЅЕуЮЊ![]() ЃЎзѓЁЂгвНЙЕуЗжБ№ЮЊ
ЃЎзѓЁЂгвНЙЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЧвДЙжБгк
ЧвДЙжБгк![]() жсЕФжБЯпНЛЭждВгкЕу
жсЕФжБЯпНЛЭждВгкЕу![]() ЃЈ
ЃЈ![]() дкЕкЯѓЯоЃЉЃЌжБЯп
дкЕкЯѓЯоЃЉЃЌжБЯп![]() ЕФаБТЪЮЊ
ЕФаБТЪЮЊ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬ;
ЕФБъзМЗНГЬ;
ЃЈ2ЃЉЙ§Еу![]() ЕФжБЯпгыЭждВНЛгк
ЕФжБЯпгыЭждВНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЈ
СНЕуЃЈ![]() ЁЂ
ЁЂ![]() ВЛгы
ВЛгы![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌШє
жиКЯЃЉЃЌШє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЗНГЬЃЎ
ЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌ
ЃЌ![]() .ЯжНЋ
.ЯжНЋ![]() би
би![]() ЗелжС
ЗелжС![]() ЃЌЕУЫФРтзЖ.
ЃЌЕУЫФРтзЖ.![]()
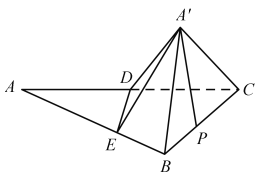
ЃЈ1ЃЉжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЧажЕ
ЫљГЩНЧЕФе§ЧажЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЖд
ЃЌЖд![]() ЁЪ[0ЃЌ Іа]ЃЌЖМга
ЁЪ[0ЃЌ Іа]ЃЌЖМга![]() ЃЌТњзуf(x2)=0ЕФЪЕЪ§xгаЧвжЛга3ИіЃЌИјГіЯТЪіЫФИіНсТл:ЂйТњзуЬтФПЬѕМўЕФЪЕЪ§x0гаЧвжЛга1ИіЃЛЂкТњзуЬтФПЬѕМўЕФЪЕЪ§x1гаЧвжЛга1ИіЃЛЂлf(x)дк
ЃЌТњзуf(x2)=0ЕФЪЕЪ§xгаЧвжЛга3ИіЃЌИјГіЯТЪіЫФИіНсТл:ЂйТњзуЬтФПЬѕМўЕФЪЕЪ§x0гаЧвжЛга1ИіЃЛЂкТњзуЬтФПЬѕМўЕФЪЕЪ§x1гаЧвжЛга1ИіЃЛЂлf(x)дк![]() ЩЯЕЅЕїЕндіЃЛЂм
ЩЯЕЅЕїЕндіЃЛЂм![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЛЦфжаЫљгае§ШЗНсТлЕФБрКХЪЧЃЈ ЃЉ
ЃЛЦфжаЫљгае§ШЗНсТлЕФБрКХЪЧЃЈ ЃЉ
A.ЂйЂлB.ЂкЂмC.ЂйЂкЂмD.ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњЪЋДЪДѓЛсЕФВЅГів§ЗЂСЫШЋУёЖСЪщШШЃЌФГбЇаЃгяЮФРЯЪІдкАрРяПЊеЙСЫвЛДЮЪЋДЪФЌаДБШШќЃЌАрРя40УћбЇЩњЕУЗжЪ§ОнЕФОЅвЖЭМШчгвЭМЃЌШєЙцЖЈЕУЗжВЛЕЭгк85ЗжЕФбЇЩњЕУЕНЁАЪЋДЪДяШЫЁБЕФГЦКХЃЌЕЭгк85ЗжЧвВЛЕЭгк70ЗжЕФбЇЩњЕУЕНЁАЪЋДЪФмЪжЁБЕФГЦКХЃЌЦфЫћбЇЩњЕУЕНЁАЪЋДЪАЎКУепЁБЕФГЦКХ.ИљОнИУДЮБШШќЕФГЩМЈАДееГЦКХЕФВЛЭЌНјааЗжВуГщбљГщбЁ10УћбЇЩњЃЌдђГщбЁЕФбЇЩњжаЛёЕУЁАЪЋДЪФмЪжЁБГЦКХЕФШЫЪ§ЮЊЃЈЁЁЁЁЃЉ

A. 6B. 5C. 4D. 2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжааФдкдЕуЃЌНЙЕудкxжсЩЯЕФЭждВЃЌРыаФТЪ![]() ЃЌЧвОЙ§ХзЮяЯп
ЃЌЧвОЙ§ХзЮяЯп![]() ЕФНЙЕуЃЎШєЙ§Еу
ЕФНЙЕуЃЎШєЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() аБТЪВЛЕШгкСу
аБТЪВЛЕШгкСу![]() гыЭждВНЛгкВЛЭЌЕФСНЕуEЁЂ
гыЭждВНЛгкВЛЭЌЕФСНЕуEЁЂ![]() дкBЁЂFжЎМф
дкBЁЂFжЎМф![]() ЃЌ
ЃЌ
![]() ЧѓЭждВЕФБъзМЗНГЬЃЛ
ЧѓЭждВЕФБъзМЗНГЬЃЛ
![]() ЧѓжБЯпlаБТЪЕФШЁжЕЗЖЮЇЃЛ
ЧѓжБЯпlаБТЪЕФШЁжЕЗЖЮЇЃЛ
![]() Шє
Шє![]() гы
гы![]() УцЛ§жЎБШЮЊ
УцЛ§жЎБШЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНЬхABCDЃA1B1C1D1жаЃЌEЁЂFЁЂGЗжБ№ЮЊAA1ЁЂBCЁЂC1D1ЕФжаЕуЃЌЯжгаЯТУцШ§ИіНсТлЃКЂйЁїEFGЮЊе§Ш§НЧаЮЃЛЂквьУцжБЯпA1GгыC1FЫљГЩНЧЮЊ60ЁуЃЛЂлACЁЮЦНУцEFG.ЦфжаЫљгае§ШЗНсТлЕФБрКХЪЧЃЈ ЃЉ
A.ЂйB.ЂкЂлC.ЂйЂкD.ЂйЂл
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com