
【题目】随机取一个由0和1构成的8位数,它的偶数位数字之和与奇数位数字之和相等的概率为____________ .
【答案】![]()
【解析】
该8位数首位数字必须为1,分别计算出奇数位上和偶数位上1的个数,结合组合知识求出基本事件总数和偶数位数字之和与奇数位数字之和相等包含的基本事件个数即可得解.
设n是满足题意的8位数,故知其偶数位上1的个数和在奇数位上1的个数相同,从而在奇数位上与偶数位上1的个数可能为1、2、3或4.注意到首位为1,下面分情况讨论:
(1)奇数位上与偶数位上有1个1,3个0共有![]() 种可能;
种可能;
(2)奇数位上与偶数位上有2个1,2个0,共有![]() 种可能;
种可能;
(3)奇数位上与偶数位上有3个1,1个0,有![]() 种可能;
种可能;
(4)奇数位上与偶数位上有4个1,共有![]() 种可能.
种可能.
合计共有4+18+12+1=35个满足条件的自然数n.又因为0和1构成的8位数共有![]() 个,从而概率为
个,从而概率为![]() .
.
故答案为:![]()


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
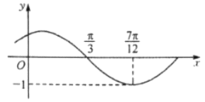
【题目】函数![]() 的图象如图所示,先将函数
的图象如图所示,先将函数![]() 图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移
图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,下列结论正确的是( )
的图象,下列结论正确的是( )
A.函数![]() 是奇函数B.函数
是奇函数B.函数![]() 在区间
在区间![]() 上是增函数
上是增函数
C.函数![]() 图象关于
图象关于![]() 对称D.函数
对称D.函数![]() 图象关于直线
图象关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为矩形,点A、E、B、F共面,![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 若平面
若平面![]() ⊥平面
⊥平面![]()
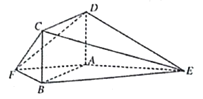
(Ⅰ)证明:平面![]() 平面ADF
平面ADF
(Ⅱ)问在线段EC上是否存在一点G,使得BG∥平面![]() 若存在,求出此时三棱锥G一ABE与三棱锥
若存在,求出此时三棱锥G一ABE与三棱锥![]() 的体积之比,若不存在,请说明理由.
的体积之比,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上的点
上的点![]() 到焦点的距离为
到焦点的距离为![]() .
.

(1)求![]() 的值;
的值;
(2)如上图,已知动线段![]() (
(![]() 在
在![]() 的右边)在直线
的右边)在直线![]() 上,且
上,且![]() ,现过
,现过![]() 作
作![]() 的切线,取左边的切点
的切线,取左边的切点![]() ,过
,过![]() 作
作![]() 的切线,取右边的切点为
的切线,取右边的切点为![]() ,当
,当![]() ,求
,求![]() 点的横坐标
点的横坐标![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,__________,求△
,__________,求△![]() 的周长
的周长![]() 和面积
和面积![]() .
.
在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线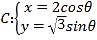 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com