
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| 3π |
| 2 |
| 3 |
| 1+cos2ωx |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 2π |
| 2ω |
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
2x+
| 0 |
| π |
| 2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| y |
|
|
| -
|
|
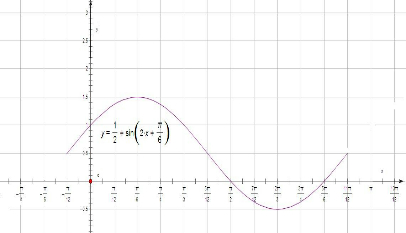
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
 侧棱垂直底面的三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1=2,点O,M分别是BC,A1C1的中点,建立如图所示空间直角坐标系.
侧棱垂直底面的三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1=2,点O,M分别是BC,A1C1的中点,建立如图所示空间直角坐标系.| CM |
| BA1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知D、E分别为△ABC的边AB、AC上的点,F是线段DE上的任意一点,DE∥BC,且S△ABC=1,求证:△BDF和△CEF中至少有一个三角形的面积不大于
如图,已知D、E分别为△ABC的边AB、AC上的点,F是线段DE上的任意一点,DE∥BC,且S△ABC=1,求证:△BDF和△CEF中至少有一个三角形的面积不大于| 1 |
| 8 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
设p:(x-2)(y-5)≠0;q:x≠2或y≠5;r:x+y≠7;则下列命题:
①p是r的既不充分也不必要条件;②p是q的充分不必要条件;③q是r的必要不充分条件.
其中全部真命题有( )
A. ①② B. ①③ C. ②③ D.①②③
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
设曲线y=ax―ln(x+1)在点(0,0)处的切线方程为y=2x,则a= ( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com